First Five Multiples Of 25
thesills
Sep 17, 2025 · 6 min read
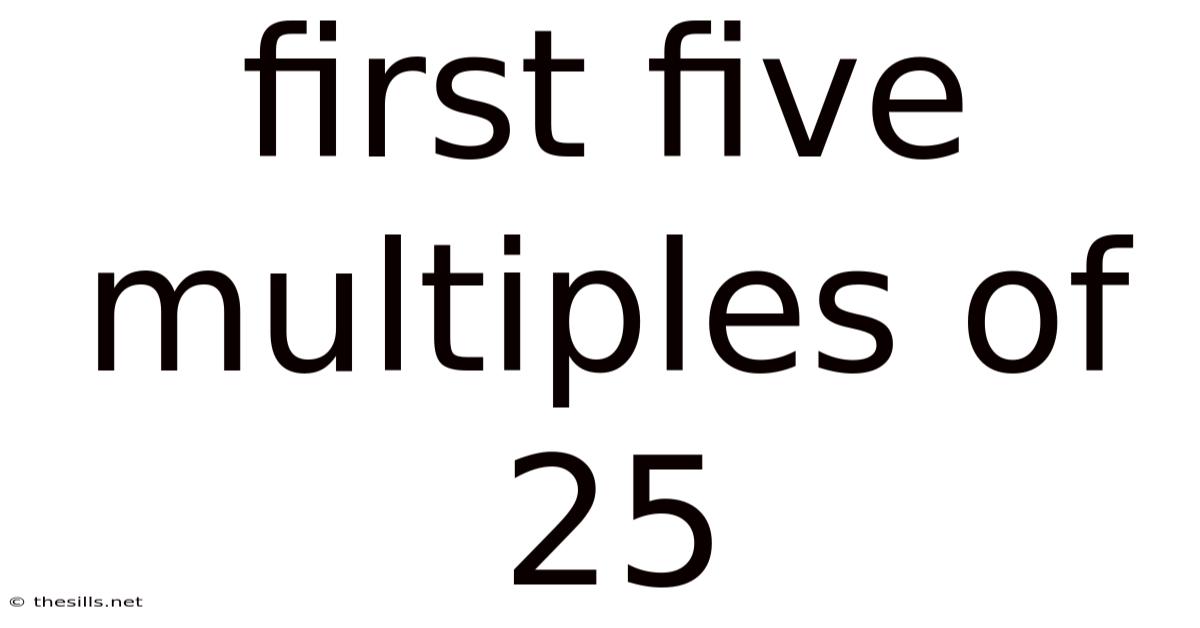
Table of Contents
Unveiling the First Five Multiples of 25: A Deep Dive into Multiplication and Number Theory
Understanding multiples is a foundational concept in mathematics, crucial for various applications from simple arithmetic to complex algebraic equations. This article delves into the fascinating world of multiples, focusing specifically on the first five multiples of 25. We'll explore their calculation, properties, real-world applications, and delve into some related mathematical concepts. This comprehensive guide will leave you with a solid grasp of multiples and their significance in mathematics.
Introduction: What are Multiples?
Before we jump into the specifics of the first five multiples of 25, let's establish a clear understanding of what a multiple is. A multiple of a number is the product of that number and any whole number (integer). In simpler terms, it's the result you get when you multiply a number by another whole number. For instance, multiples of 2 include 2 (2 x 1), 4 (2 x 2), 6 (2 x 3), and so on. Each of these numbers is a multiple of 2 because they are all obtained by multiplying 2 by a whole number.
Calculating the First Five Multiples of 25
Now, let's focus on our main subject: the first five multiples of 25. To find these, we simply multiply 25 by the first five whole numbers (0, 1, 2, 3, and 4). This gives us:
- 0 x 25 = 0 (the zero multiple)
- 1 x 25 = 25 (the first multiple)
- 2 x 25 = 50 (the second multiple)
- 3 x 25 = 75 (the third multiple)
- 4 x 25 = 100 (the fourth multiple)
Therefore, the first five multiples of 25 are 0, 25, 50, 75, and 100. Note that many sources will exclude zero. This is valid; it depends on the context of the problem.
Properties of the First Five Multiples of 25
These multiples share several interesting properties:
- Divisibility by 25: Each number is perfectly divisible by 25, leaving no remainder. This is the defining characteristic of a multiple.
- Divisibility by 5: All are also divisible by 5, as 25 itself is a multiple of 5. This demonstrates the transitive property of divisibility: If a number is divisible by another number, then any multiple of the first number is also divisible by the second number.
- Pattern Recognition: Notice the consistent pattern in the units digit: 0, 5, 0, 5, 0. This alternating pattern of 0 and 5 in the units place is a characteristic of multiples of 25.
- Arithmetic Progression: These multiples form an arithmetic progression with a common difference of 25. This means that each subsequent multiple is obtained by adding 25 to the previous multiple. This property is a fundamental concept in arithmetic sequences.
Real-World Applications of Multiples of 25
Multiples of 25 appear frequently in everyday life:
- Money: Many countries use currency systems based on multiples of 25 (e.g., 25 cents, $0.50, $0.75, $1.00). This makes calculations simpler and quicker.
- Measurements: Measurements often involve multiples of 25, especially in systems using inches or centimeters. For example, rulers and tape measures frequently have markings at 25-unit intervals.
- Time: A quarter of an hour (15 minutes) is closely related to multiples of 25, as it represents 25% of an hour.
- Percentages: Calculations involving percentages frequently utilize multiples of 25, as it’s a common fraction (1/4).
Exploring Related Mathematical Concepts
Understanding multiples of 25 opens doors to a wider understanding of various mathematical concepts:
- Factors and Multiples: Multiples are closely related to factors. While multiples are the results of multiplication, factors are the numbers that divide a given number without leaving a remainder. For example, the factors of 25 are 1, 5, and 25. Notice that 25 is both a factor of itself and a multiple of 1 and 5.
- Prime Factorization: The prime factorization of 25 is 5 x 5 (5²). Understanding prime factorization is crucial for various mathematical operations, including simplifying fractions and finding least common multiples (LCM) and greatest common divisors (GCD).
- Least Common Multiple (LCM): The LCM of two or more numbers is the smallest number that is a multiple of all the numbers. Finding the LCM is essential in solving problems involving fractions and ratios. For example, finding the LCM of 25 and 10 would be useful in comparing or adding fractions with these denominators.
- Greatest Common Divisor (GCD): The GCD of two or more numbers is the largest number that divides all the numbers without leaving a remainder. GCD is often used in simplifying fractions. The GCD of 25 and 50 is 25, a crucial concept in algebra and number theory.
- Arithmetic Sequences: As mentioned earlier, the multiples of 25 form an arithmetic sequence. These sequences have a constant difference between consecutive terms. Understanding arithmetic sequences is crucial in various fields, including finance and physics.
- Geometric Sequences: While the multiples of 25 don't form a geometric sequence (a sequence with a constant ratio between consecutive terms), understanding both arithmetic and geometric sequences is vital in mathematical modeling.
The Significance of Zero as a Multiple
Including zero as a multiple of 25 might seem counterintuitive, but it's mathematically sound. Zero is a multiple of every integer because it's the product of any integer and zero (e.g., 0 x 25 = 0). This aligns with the definition of a multiple, making the inclusion of zero consistent and important in mathematical contexts. However, in some practical applications, particularly in counting or enumerating objects, zero might be omitted.
Beyond the First Five: Extending the Pattern
The pattern of multiples of 25 continues infinitely. We can predict any multiple of 25 by using the formula: 25n, where 'n' is any whole number. This allows us to easily calculate any multiple of 25, no matter how large.
Frequently Asked Questions (FAQ)
Q1: Are all multiples of 25 even numbers?
A1: No. While some multiples of 25 are even (e.g., 50, 100), others are odd (e.g., 25, 75). Whether a multiple of 25 is even or odd depends on whether 'n' in the formula 25n is even or odd.
Q2: How can I quickly identify a multiple of 25?
A2: A number is a multiple of 25 if it ends in 00, 25, 50, or 75. This is a quick way to identify multiples of 25 without performing a division.
Q3: What is the 10th multiple of 25?
A3: Using the formula 25n, where n=10, the 10th multiple of 25 is 25 x 10 = 250.
Q4: What is the relationship between multiples and divisibility?
A4: A number is a multiple of another number if it is divisible by that number without leaving a remainder. Divisibility is a key characteristic of multiples.
Conclusion: The Enduring Importance of Multiples
Understanding multiples is more than just memorizing multiplication facts. It’s about grasping a fundamental concept that underpins a wide range of mathematical ideas. The first five multiples of 25, seemingly simple at first glance, provide a gateway to exploring deeper concepts like divisibility, prime factorization, arithmetic sequences, and their diverse applications in the real world. Mastering this foundational concept empowers you to navigate more complex mathematical challenges with confidence and proficiency. From everyday calculations to advanced mathematical modeling, the significance of understanding multiples, and the properties of numbers like 25, cannot be overstated. Keep exploring, keep learning, and keep discovering the beauty and power of mathematics!
Latest Posts
Latest Posts
-
Arctan Of 1 Sqrt 3
Sep 18, 2025
-
Integration Of 4 X 2
Sep 18, 2025
-
Hard Water And Soap Scum
Sep 18, 2025
-
What Is 15 Of 500
Sep 18, 2025
-
Is 196 A Square Number
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about First Five Multiples Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.