Factor X 2 X 72
thesills
Sep 16, 2025 · 6 min read
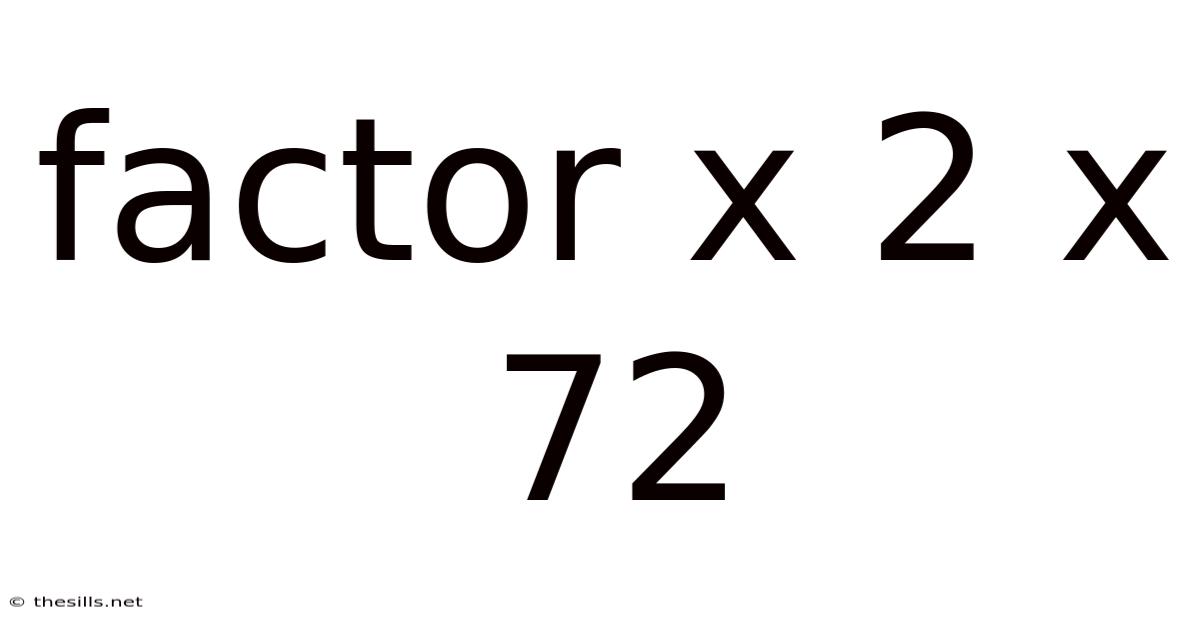
Table of Contents
Unraveling the Mystery of Factor x 2 x 72: A Deep Dive into Multiplication and Factorization
This article explores the mathematical concept behind the expression "Factor x 2 x 72," delving into the meaning of factors, prime factorization, and the various ways to approach this seemingly simple yet conceptually rich problem. We'll cover fundamental mathematical principles, practical applications, and even touch upon the historical context surrounding factorization. Understanding this seemingly basic calculation opens doors to more complex algebraic manipulations and problem-solving strategies. This guide aims to provide a comprehensive understanding, suitable for learners of all levels.
What are Factors?
Before we tackle "Factor x 2 x 72," let's establish a firm understanding of what factors are. In mathematics, a factor is a number that divides another number without leaving a remainder. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, because each of these numbers divides 12 evenly. Finding all the factors of a number is a crucial step in many mathematical operations, including simplifying fractions, solving equations, and understanding algebraic expressions.
Think of factors as the building blocks of a number. Just as you can build a house from bricks, you can construct a number by multiplying its factors together. The process of finding these building blocks is called factorization.
Prime Factorization: The Foundation of Factorization
Prime factorization is a special type of factorization where we break down a number into its prime factors. A prime number is a whole number greater than 1 that has only two factors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely represented as a product of prime numbers, disregarding the order of the factors. This unique representation is known as the prime factorization of the number.
For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3). We can't break these factors down any further into smaller prime numbers. Prime factorization is a fundamental concept in number theory and is used extensively in various mathematical fields.
Decomposing 72: Finding its Prime Factors
To fully understand "Factor x 2 x 72," we need to find the prime factorization of 72. We can do this using a factor tree:
- Start with 72.
- Notice that 72 is an even number, so it's divisible by 2. 72 ÷ 2 = 36.
- 36 is also even, so it's divisible by 2. 36 ÷ 2 = 18.
- 18 is even, divisible by 2. 18 ÷ 2 = 9.
- 9 is not divisible by 2, but it is divisible by 3. 9 ÷ 3 = 3.
- 3 is a prime number.
Therefore, the prime factorization of 72 is 2 x 2 x 2 x 3 x 3, or 2³ x 3².
Solving "Factor x 2 x 72"
Now that we've understood factors and prime factorization, let's return to the expression "Factor x 2 x 72." The problem is incomplete; we need to know what "Factor" represents. It's a variable, a placeholder for an unknown number. Let's explore different scenarios:
Scenario 1: Finding a Missing Factor
If the problem implies finding a missing factor that, when multiplied by 2 and 72, results in a specific number, we need additional information. For example:
- "Factor x 2 x 72 = 864"
To find the missing factor, we would divide 864 by (2 x 72):
864 ÷ (2 x 72) = 864 ÷ 144 = 6
In this case, the missing factor is 6.
Scenario 2: Exploring Factors of the Product
If the problem asks to find all the factors of the product (2 x 72 = 144), we need to find all numbers that divide 144 evenly. This involves finding the prime factorization of 144 and then systematically generating all possible combinations of its factors.
The prime factorization of 144 is 2⁴ x 3². To find all factors, we consider all possible combinations of powers of 2 (from 2⁰ to 2⁴) and powers of 3 (from 3⁰ to 3²):
- 2⁰ x 3⁰ = 1
- 2¹ x 3⁰ = 2
- 2² x 3⁰ = 4
- 2³ x 3⁰ = 8
- 2⁴ x 3⁰ = 16
- 2⁰ x 3¹ = 3
- 2¹ x 3¹ = 6
- 2² x 3¹ = 12
- 2³ x 3¹ = 24
- 2⁴ x 3¹ = 48
- 2⁰ x 3² = 9
- 2¹ x 3² = 18
- 2² x 3² = 36
- 2³ x 3² = 72
- 2⁴ x 3² = 144
Therefore, the factors of 144 are 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, and 144.
Scenario 3: Simplifying Algebraic Expressions
In algebra, "Factor x 2 x 72" might represent a term in an equation. Simplifying this term involves multiplying the known numbers together:
Factor x 144
This simplified form highlights the unknown factor and prepares the expression for further algebraic manipulations, such as solving for the value of "Factor" within a larger equation.
Real-World Applications
Understanding factors and factorization extends beyond theoretical mathematics. Here are some real-world applications:
- Geometry: Calculating the area or volume of shapes often involves factoring.
- Computer Science: Cryptography relies heavily on prime factorization for secure data encryption.
- Engineering: Factorization is used in structural analysis and design.
- Finance: Calculating compound interest and loan repayments often involves using factors.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a factor and a multiple?
A factor divides a number evenly, while a multiple is the result of multiplying a number by an integer. For example, 3 is a factor of 12 (12 ÷ 3 = 4), and 12 is a multiple of 3 (3 x 4 = 12).
Q2: How can I find the prime factorization of a large number?
For larger numbers, you can use a systematic approach. Divide the number by the smallest prime number (2) repeatedly until you get an odd number. Then, try dividing by 3, 5, 7, and other prime numbers until you reach 1.
Q3: Why is prime factorization important?
Prime factorization is fundamental because it provides a unique representation of any number. This unique representation is crucial for various mathematical operations and algorithms.
Q4: Are there any shortcuts for finding factors?
There are divisibility rules that can help you quickly determine if a number is divisible by certain prime numbers (e.g., a number is divisible by 3 if the sum of its digits is divisible by 3).
Conclusion
The expression "Factor x 2 x 72" initially appears simple, but its exploration reveals the rich tapestry of mathematical concepts underlying factorization. Understanding factors, prime factorization, and their applications extends beyond solving simple arithmetic problems. It forms a cornerstone for more advanced mathematical concepts, providing a fundamental building block for problem-solving across various disciplines. This deep dive highlights the importance of not just obtaining an answer, but understanding the underlying principles and appreciating the interconnectedness of mathematical concepts. Whether you're a student grappling with early algebra or a seasoned mathematician, a firm grasp of factorization provides a powerful tool for tackling numerous mathematical challenges.
Latest Posts
Latest Posts
-
Difference Between Parallelogram And Rhombus
Sep 16, 2025
-
Vintage Spinning Wheel For Sale
Sep 16, 2025
-
Is Hg2i2 Soluble In Water
Sep 16, 2025
-
What Is A Global Grid
Sep 16, 2025
-
The Units Of Momentum Are
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 X 72 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.