Factor X 2 5x 6
thesills
Sep 17, 2025 · 6 min read
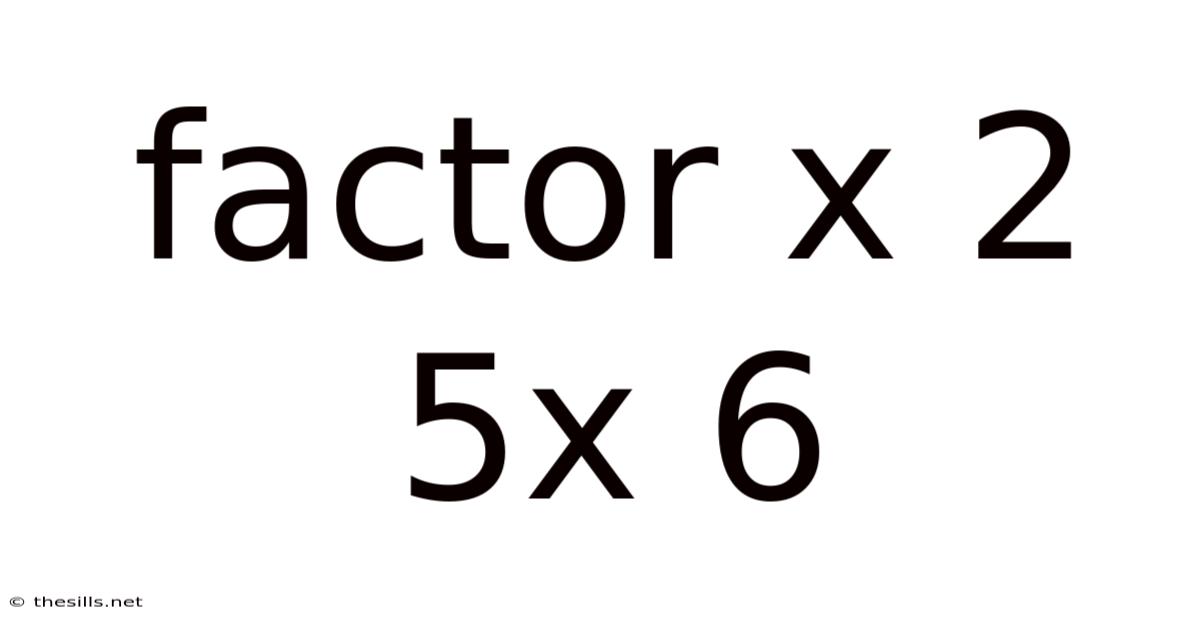
Table of Contents
Factoring the Quadratic Expression: x² + 5x + 6
Understanding how to factor quadratic expressions is a fundamental skill in algebra. This seemingly simple expression, x² + 5x + 6, provides an excellent opportunity to explore various factoring techniques and delve into the underlying mathematical principles. This comprehensive guide will take you through the process step-by-step, explaining not just how to factor but also why these methods work. We'll cover multiple approaches, address common misconceptions, and even explore the connection to graphical representations. By the end, you'll be confident in factoring similar quadratic expressions and understand the broader implications of this algebraic manipulation.
Introduction: What is Factoring?
Factoring, in the context of algebra, is the process of rewriting an expression as a product of simpler expressions. Think of it like reverse multiplication. Just as 2 x 3 = 6, factoring 6 would give you 2 and 3 as its factors. Similarly, factoring a quadratic expression like x² + 5x + 6 involves finding two binomial expressions that, when multiplied, result in the original quadratic. This skill is crucial for solving quadratic equations, simplifying expressions, and understanding various mathematical concepts.
Method 1: The AC Method (for trinomials of the form ax² + bx + c)
Our expression, x² + 5x + 6, is a trinomial (three terms) where a = 1, b = 5, and c = 6. The AC method is particularly useful for factoring quadratics where 'a' is not equal to 1. However, it works perfectly well even when a = 1, as in our case.
-
Find the product AC: In our case, A * C = 1 * 6 = 6.
-
Find two numbers that add up to B and multiply to AC: We need two numbers that add up to 5 (our 'b' value) and multiply to 6. These numbers are 2 and 3 (2 + 3 = 5 and 2 * 3 = 6).
-
Rewrite the middle term: Replace the middle term (5x) with the two numbers we found: x² + 2x + 3x + 6
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair: x(x + 2) + 3(x + 2)
-
Factor out the common binomial: Notice that both terms now share the binomial (x + 2). Factor this out: (x + 2)(x + 3)
Therefore, the factored form of x² + 5x + 6 is (x + 2)(x + 3).
Method 2: Trial and Error (for simpler trinomials)
For simpler quadratics where a = 1, the trial and error method can be quicker. It relies on understanding how binomial multiplication works.
-
Set up the binomial factors: Since a = 1, we know the first terms of our binomial factors will be 'x': (x )(x )
-
Find factors of 'c': The constant term, c, is 6. Find pairs of factors of 6: (1, 6) and (2, 3).
-
Test the combinations: We need the factors to add up to our 'b' value (5). Let's try the pairs:
- (x + 1)(x + 6): When expanded, this gives x² + 7x + 6 (incorrect)
- (x + 2)(x + 3): When expanded, this gives x² + 5x + 6 (correct!)
This confirms that the factored form is (x + 2)(x + 3).
Method 3: Using the Quadratic Formula (for solving, not directly factoring)
While not a direct factoring method, the quadratic formula can help find the roots of the quadratic equation x² + 5x + 6 = 0. These roots are the values of x that make the equation true. Knowing the roots helps us deduce the factored form.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
For our equation: a = 1, b = 5, c = 6
x = [-5 ± √(5² - 4 * 1 * 6)] / 2 * 1 x = [-5 ± √1] / 2 x = (-5 + 1) / 2 = -2 or x = (-5 - 1) / 2 = -3
The roots are -2 and -3. Therefore, the factored form is (x + 2)(x + 3), since (x - (-2)) = (x + 2) and (x - (-3)) = (x + 3).
The Significance of Factoring
Factoring quadratic expressions is more than just an algebraic manipulation; it unlocks several important applications:
-
Solving Quadratic Equations: Setting the factored expression equal to zero allows us to solve for x using the zero-product property (if AB = 0, then either A = 0 or B = 0). This is essential for finding the x-intercepts (roots) of a parabola.
-
Simplifying Expressions: Factoring can simplify complex algebraic expressions, making them easier to work with. This is particularly useful in calculus and other advanced mathematical fields.
-
Graphing Parabolas: The factored form reveals the x-intercepts of the parabola represented by the quadratic equation. This information, along with the vertex, helps in accurately sketching the parabola.
-
Understanding Quadratic Relationships: Factoring provides insight into the underlying relationship between variables in quadratic models used in various fields like physics, engineering, and economics.
Common Mistakes to Avoid
-
Incorrect signs: Be careful with the signs when factoring. Double-check your expansion to ensure it matches the original expression.
-
Missing factors: Carefully consider all possible factor pairs of the constant term.
-
Incorrect grouping: When using the AC method, ensure the terms are grouped correctly to facilitate factoring.
-
Forgetting to check: Always expand your factored expression to verify it equals the original quadratic.
Frequently Asked Questions (FAQ)
-
What if the quadratic expression cannot be factored? Not all quadratic expressions can be factored using integers. In such cases, the quadratic formula or completing the square can be used to find the roots.
-
Can I factor a quadratic expression with a coefficient other than 1 for the x² term? Yes, the AC method is specifically designed for such cases. You will follow the same steps but will need to consider the coefficient of x² when finding the factors.
-
What is the difference between factoring and solving a quadratic equation? Factoring is a process of rewriting an expression as a product of simpler expressions. Solving a quadratic equation involves finding the values of the variable that make the equation true. Factoring is often a step in solving quadratic equations.
-
How can I improve my factoring skills? Practice is key! Work through numerous examples, starting with simple expressions and gradually increasing the complexity. Understand the underlying logic behind each method.
Conclusion: Mastering the Art of Factoring
Factoring the quadratic expression x² + 5x + 6, seemingly a simple task, provides a gateway to a deeper understanding of algebra and its applications. By mastering the techniques discussed – the AC method, trial and error, and understanding the connection to the quadratic formula – you'll gain confidence in manipulating quadratic expressions and solving related equations. Remember that consistent practice and a thorough understanding of the underlying principles are essential to mastering this fundamental algebraic skill. Don't be afraid to explore different methods and find the one that best suits your learning style. The ability to factor quadratic expressions is a building block for success in higher-level mathematics and related fields.
Latest Posts
Latest Posts
-
Carbon Formula In Standard State
Sep 17, 2025
-
Atm To N Cm 2
Sep 17, 2025
-
Is South America Latin America
Sep 17, 2025
-
Convert 300 Kelvin Into Celsius
Sep 17, 2025
-
Convert 330 Degrees To Radians
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Factor X 2 5x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.