Factor X 2 5x 14
thesills
Sep 14, 2025 · 6 min read
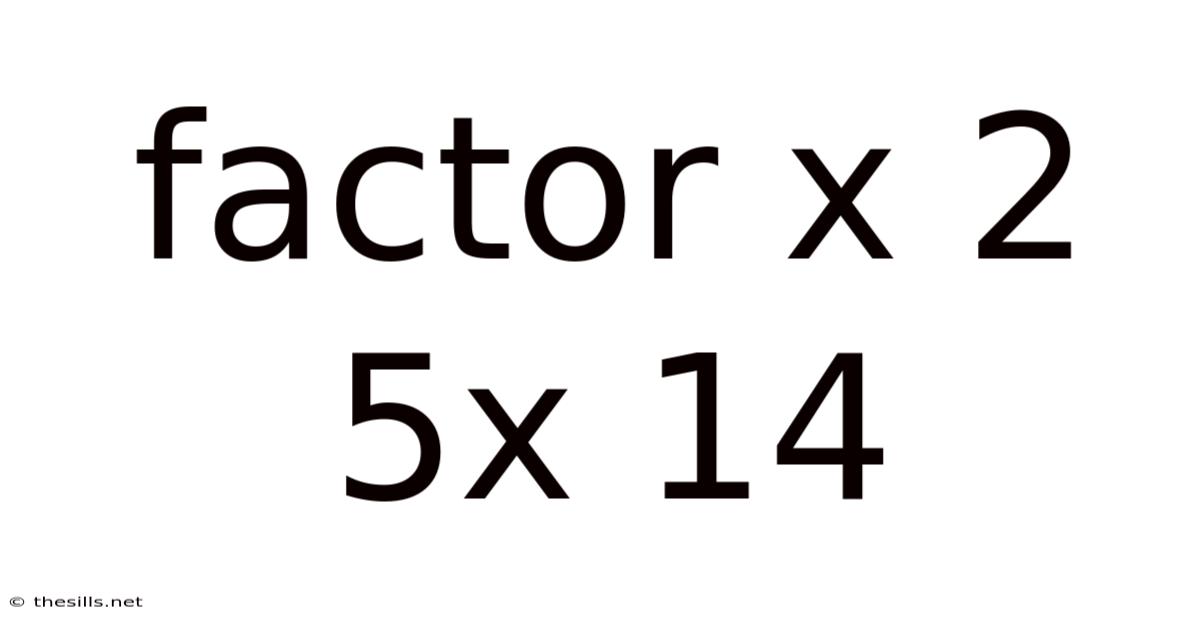
Table of Contents
Factoring the Quadratic Expression: x² + 5x + 14
This article delves into the process of factoring the quadratic expression x² + 5x + 14. We'll explore various methods, discuss the concept of factoring in general, and examine why this particular expression presents a unique challenge. Understanding how to factor quadratics is fundamental in algebra, laying the groundwork for solving equations, graphing parabolas, and tackling more complex mathematical problems. We'll also address common misconceptions and provide a step-by-step approach that's easy to follow, regardless of your mathematical background.
Introduction: What is Factoring?
Factoring, in the context of algebra, is the process of breaking down a mathematical expression into simpler components that, when multiplied together, yield the original expression. Think of it like reverse multiplication. For example, factoring the number 12 might involve finding its factors: 2 x 6, 3 x 4, or 1 x 12. Similarly, factoring a quadratic expression like x² + 5x + 14 involves finding two binomial expressions that, when multiplied, result in the original quadratic. This process is crucial for simplifying expressions, solving equations, and understanding the underlying structure of polynomial functions.
Attempting to Factor x² + 5x + 14: The Challenge
The quadratic expression x² + 5x + 14 presents a unique challenge because it's not readily factorable using the standard methods typically taught in introductory algebra courses. Let's examine the usual approach:
-
Looking for Common Factors: There are no common factors among the terms x², 5x, and 14. This means we can't simplify the expression by factoring out a common number or variable.
-
The Standard Trinomial Factoring Method: This method involves finding two numbers that add up to the coefficient of the x term (5 in this case) and multiply to the constant term (14). Let's try to find such numbers:
-
Pairs of factors of 14: (1, 14), (2, 7), (-1, -14), (-2, -7)
-
None of these pairs add up to 5.
-
This indicates that the expression x² + 5x + 14 cannot be factored using integers. This is a crucial point. Not all quadratic expressions are factorable using integers.
Understanding Irreducible Quadratics
A quadratic expression that cannot be factored using integers is called an irreducible quadratic. This doesn't mean the expression is useless or meaningless; it simply means that its simplest form is the original quadratic itself. It's important to understand that irreducibility is relative to the number system you're working with. In this case, x² + 5x + 14 is irreducible over the integers, but we might be able to factor it using other number systems (such as complex numbers), but that’s beyond the scope of this introductory discussion.
Alternative Approaches: The Quadratic Formula and Completing the Square
Since factoring with integers isn't possible, we can resort to other methods to analyze and work with this quadratic expression. Two common approaches are:
-
The Quadratic Formula: This powerful formula provides the solutions (roots) to any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = (-b ± √(b² - 4ac)) / 2a
For our expression, a = 1, b = 5, and c = 14. Plugging these values into the quadratic formula gives us:
x = (-5 ± √(5² - 4 * 1 * 14)) / 2 * 1 x = (-5 ± √(25 - 56)) / 2 x = (-5 ± √(-31)) / 2
Notice that we have a negative number under the square root. This indicates that the roots of the quadratic equation x² + 5x + 14 = 0 are complex numbers. The solutions involve the imaginary unit i, where i² = -1. The solutions are approximately x ≈ -2.5 ± 2.78i.
-
Completing the Square: This method involves manipulating the quadratic expression to create a perfect square trinomial, which can then be easily factored. The process is more involved and is best explained with a step-by-step example:
-
Move the constant term: Rewrite the expression as x² + 5x = -14.
-
Find the value to complete the square: Take half of the coefficient of the x term (5/2 = 2.5), square it (2.5² = 6.25), and add it to both sides of the equation:
x² + 5x + 6.25 = -14 + 6.25 x² + 5x + 6.25 = -7.75
-
Factor the perfect square trinomial: The left side is now a perfect square trinomial: (x + 2.5)² = -7.75
-
Solve for x: Take the square root of both sides, remembering to consider both positive and negative square roots:
x + 2.5 = ±√(-7.75) x = -2.5 ± √(-7.75) (Again, involving complex numbers)
-
Graphical Representation
The fact that the quadratic equation x² + 5x + 14 = 0 has complex roots means that the parabola representing the quadratic function y = x² + 5x + 14 does not intersect the x-axis. The parabola opens upwards (because the coefficient of x² is positive) and lies entirely above the x-axis. This visual representation reinforces the conclusion that the quadratic expression is irreducible over the real numbers.
Conclusion: The Significance of Irreducible Quadratics
While x² + 5x + 14 cannot be factored using integers, its irreducibility doesn't diminish its importance in algebra. Understanding the concept of irreducible quadratics is crucial for a comprehensive grasp of quadratic equations and their solutions. The fact that it leads to complex roots opens the door to a deeper exploration of number systems and the richness of mathematical concepts. Mastering techniques like the quadratic formula and completing the square enables you to handle a wider range of quadratic expressions, paving the way for tackling more advanced algebraic concepts.
Frequently Asked Questions (FAQ)
-
Q: Why is it important to know if a quadratic is factorable?
A: Factoring simplifies expressions, making them easier to work with. It's essential for solving quadratic equations, finding the roots, and analyzing the behavior of quadratic functions.
-
Q: Are all quadratic expressions factorable?
A: No, not all quadratic expressions are factorable using integers. Some, like x² + 5x + 14, are irreducible over the real numbers.
-
Q: What if I get a negative number under the square root when using the quadratic formula?
A: A negative number under the square root indicates that the roots of the quadratic equation are complex numbers, involving the imaginary unit i.
-
Q: Is completing the square always easier than the quadratic formula?
A: Not necessarily. The quadratic formula is a more general and often quicker method for solving quadratic equations, especially when the coefficients are not easily manipulated for completing the square. Completing the square, however, provides valuable insight into the structure of the quadratic.
-
Q: Can I use a calculator or software to factor quadratics?
A: While calculators and software can help solve quadratic equations and find roots, understanding the underlying methods (factoring, quadratic formula, completing the square) is vital for a deep understanding of algebra. These tools should be used to verify your work, not replace your understanding of the process.
This comprehensive exploration of the quadratic expression x² + 5x + 14 demonstrates the importance of understanding not only how to factor quadratics but also what to do when standard factoring techniques fail. It highlights the use of alternative methods and the significance of complex numbers in the field of algebra. Through understanding these concepts, you can build a stronger foundation for tackling more advanced mathematical challenges.
Latest Posts
Related Post
Thank you for visiting our website which covers about Factor X 2 5x 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.