Factor 6x 2 X 2
thesills
Sep 17, 2025 · 6 min read
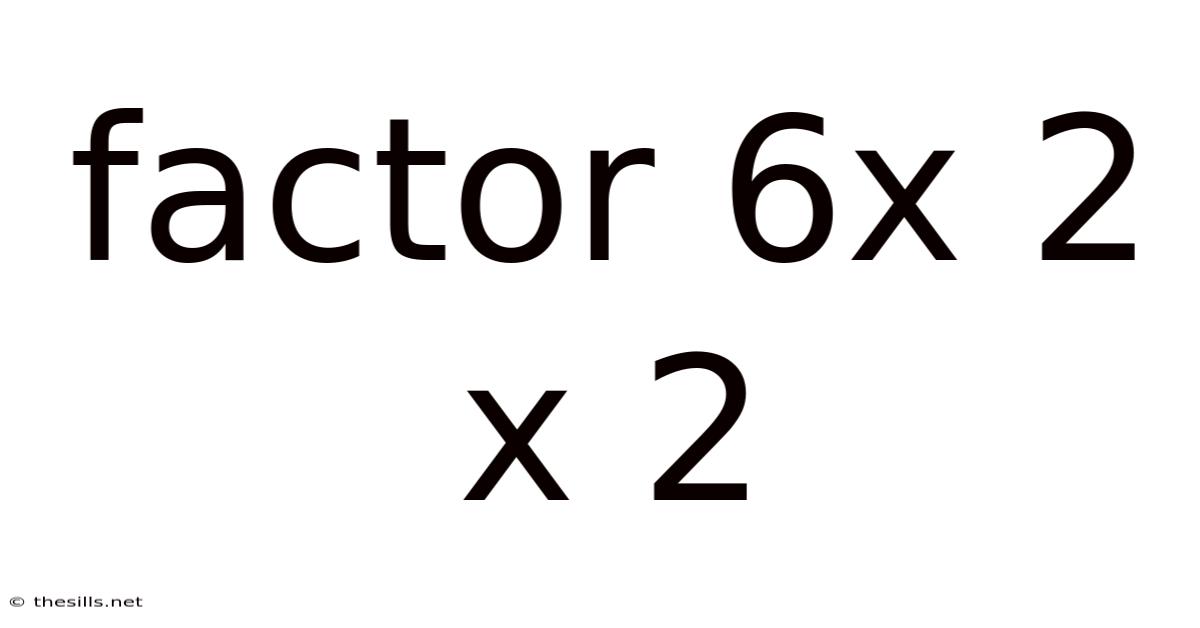
Table of Contents
Unraveling the Mystery: A Deep Dive into Factoring 6x² + 2x + 2
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor allows you to simplify expressions, solve equations, and delve deeper into the world of mathematical relationships. This article will thoroughly explore the process of factoring the quadratic expression 6x² + 2x + 2, covering various methods, explaining the underlying principles, and answering frequently asked questions. We'll move beyond simply finding the answer to understanding why the answer is what it is, equipping you with a solid foundation in algebraic manipulation.
Understanding Quadratic Expressions
Before diving into the factoring process, let's refresh our understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (typically 'x') is 2. The general form of a quadratic expression is ax² + bx + c, where 'a', 'b', and 'c' are constants (numbers). In our case, 6x² + 2x + 2, we have a = 6, b = 2, and c = 2.
Attempting Traditional Factoring Methods
The most common approach to factoring quadratic expressions involves finding two binomials whose product equals the original quadratic. This often involves looking for factors of 'a' and 'c' that add up to 'b'. Let's try this approach with 6x² + 2x + 2:
We need to find two numbers that multiply to (6)(2) = 12 and add up to 2. Unfortunately, there are no such integer pairs. This indicates that our quadratic expression, 6x² + 2x + 2, cannot be factored using simple integer coefficients. This doesn't mean it's unfactorable; it simply means that the traditional methods won't work directly.
Exploring the Quadratic Formula
When simple factoring fails, we can turn to the quadratic formula, a powerful tool for finding the roots (or zeros) of any quadratic equation. The quadratic formula is derived from completing the square and provides a general solution for the equation ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
Let's apply this formula to our expression:
x = [-2 ± √(2² - 4 * 6 * 2)] / (2 * 6) x = [-2 ± √(4 - 48)] / 12 x = [-2 ± √(-44)] / 12 x = [-2 ± 2i√11] / 12 x = [-1 ± i√11] / 6
The solutions are complex numbers because the discriminant (b² - 4ac = -44) is negative. This confirms that the quadratic expression cannot be factored into real linear factors. The presence of imaginary units ('i', where i² = -1) signifies that the parabola represented by this quadratic does not intersect the x-axis.
Factoring with the Greatest Common Factor (GCF)
While we cannot factor the expression into simple binomials with real coefficients, we can simplify it by factoring out the greatest common factor (GCF). In this case, the GCF of 6x², 2x, and 2 is 2. Therefore, we can rewrite the expression as:
2(3x² + x + 1)
This simplified form is factored as much as possible using real numbers. The expression within the parentheses, 3x² + x + 1, is a prime quadratic; it cannot be factored further using real numbers.
Understanding the Discriminant and its Significance
The discriminant (b² - 4ac) in the quadratic formula holds significant information about the nature of the quadratic equation's roots:
-
Positive Discriminant: The quadratic has two distinct real roots. This means the parabola intersects the x-axis at two different points. The quadratic can be factored into two distinct linear factors with real coefficients.
-
Zero Discriminant: The quadratic has one real root (a repeated root). The parabola touches the x-axis at exactly one point. The quadratic can be factored as a perfect square trinomial.
-
Negative Discriminant: The quadratic has two complex conjugate roots (roots with imaginary parts). The parabola does not intersect the x-axis. The quadratic cannot be factored into linear factors with real coefficients.
In our case, the negative discriminant (-44) clearly indicates the presence of complex roots and the inability to factor the original expression into real linear factors.
Graphical Representation and its Implications
Visualizing the quadratic function y = 6x² + 2x + 2 graphically further solidifies our understanding. The parabola opens upwards (since a = 6 > 0) and lies entirely above the x-axis. This visual representation confirms that there are no real x-intercepts, further supporting our conclusion that the expression cannot be factored using real numbers.
Advanced Factoring Techniques (Beyond the Scope of this Expression)
While not applicable to 6x² + 2x + 2 directly due to its complex roots, it's worthwhile to briefly mention some advanced factoring techniques:
-
Completing the Square: This method involves manipulating the quadratic expression to create a perfect square trinomial, allowing for factorization.
-
Synthetic Division: Used when one or more roots are known, synthetic division allows for efficient factoring.
-
Rational Root Theorem: Helps to identify potential rational roots of a polynomial equation, guiding the factoring process.
These advanced methods are usually employed when dealing with higher-degree polynomials or when more complex factorization is required.
Frequently Asked Questions (FAQ)
Q: Why can't I factor 6x² + 2x + 2 using simple integer coefficients?
A: The combination of the coefficients (a=6, b=2, c=2) doesn't allow for finding two integers that multiply to 12 (ac) and add up to 2 (b). This is a direct consequence of the negative discriminant.
Q: Does the fact that it can't be factored into real numbers mean it's useless?
A: Absolutely not! While it can't be factored into real linear factors, the expression is still valuable in various mathematical contexts. It can be used in equations, manipulated algebraically, and analyzed using other mathematical tools. The inability to factor using real numbers simply means that its roots are complex.
Q: What does it mean to have complex roots?
A: Complex roots are solutions to an equation that involve the imaginary unit 'i' (√-1). They represent points in the complex plane, not on the real number line. In the context of our quadratic, it means the parabola never crosses the x-axis.
Q: Can I use this expression in real-world applications?
A: Yes. Quadratic equations, even with complex roots, frequently appear in physics, engineering, and other fields modeling oscillatory phenomena, wave behavior, or situations where complex numbers naturally arise.
Conclusion
Factoring the quadratic expression 6x² + 2x + 2 reveals more than just a simple algebraic manipulation. It showcases the significance of the discriminant in determining the nature of the roots, highlighting the difference between real and complex solutions. While traditional factoring methods fail here, the application of the quadratic formula and the extraction of the GCF provide a comprehensive understanding. This deep dive should not only solidify your understanding of factoring but also broaden your appreciation for the richness and complexity of algebra. Remember, even when a quadratic expression doesn't factor nicely with real numbers, it still holds valuable mathematical meaning and can find application in various contexts. The journey of exploration, from the initial attempt at simple factoring to the application of the quadratic formula and the understanding of the discriminant, is a fundamental step in mastering algebraic techniques.
Latest Posts
Latest Posts
-
What Is 4 5 In Decimal
Sep 17, 2025
-
Bio Science Subjects In 11th
Sep 17, 2025
-
How To Make An Ogive
Sep 17, 2025
-
How Does Amplitude Determine Loudness
Sep 17, 2025
-
Oxygen Ion With 10 Electrons
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Factor 6x 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.