Factor 6x 2 5x 1
thesills
Sep 14, 2025 · 6 min read
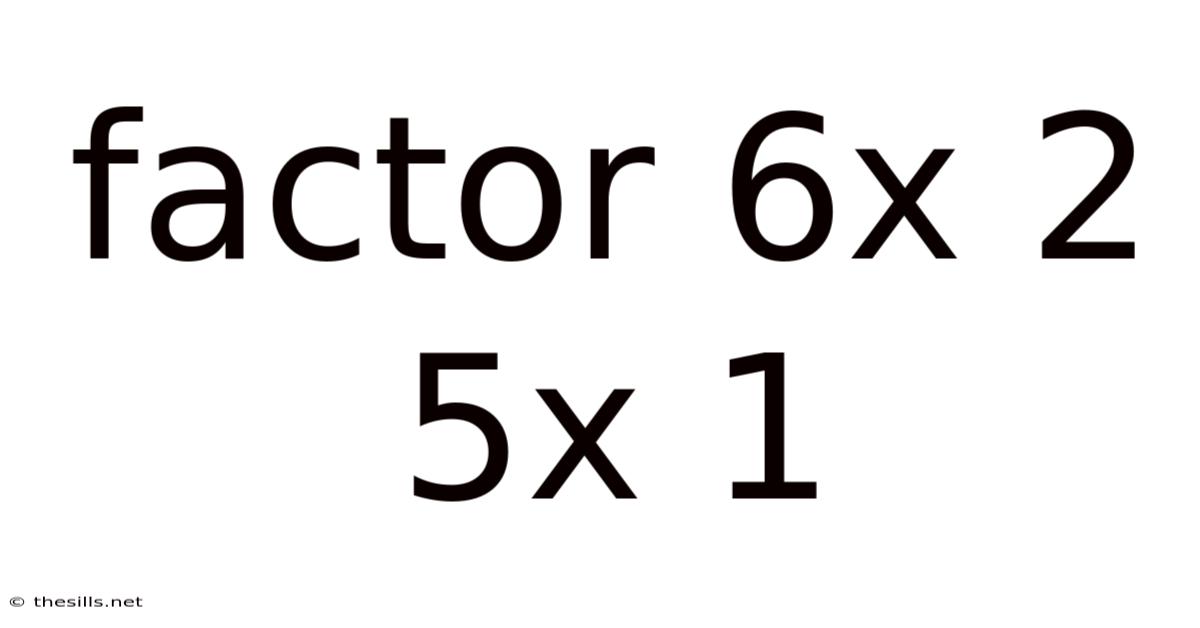
Table of Contents
Factoring the Quadratic Expression: 6x² + 5x + 1
This article delves into the complete process of factoring the quadratic expression 6x² + 5x + 1. We will explore multiple methods, providing a thorough understanding of the underlying mathematical principles and offering practical strategies for solving similar problems. Understanding quadratic factoring is crucial for various mathematical applications, including solving quadratic equations, simplifying algebraic expressions, and even in advanced calculus.
Introduction to Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (typically 'x') is 2. It takes the general form ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Factoring a quadratic expression means rewriting it as a product of two simpler expressions, usually two linear binomials. This process is fundamental in algebra and forms the basis for solving many types of equations. Our focus here is on factoring 6x² + 5x + 1.
Method 1: The AC Method (Splitting the Middle Term)
This is a widely used method for factoring quadratic trinomials. It involves finding two numbers that add up to the coefficient of the 'x' term (b) and multiply to the product of the coefficient of the x² term (a) and the constant term (c).
Steps:
-
Identify a, b, and c: In our expression, 6x² + 5x + 1, we have a = 6, b = 5, and c = 1.
-
Find the product ac: ac = 6 * 1 = 6
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 5 and multiply to 6. These numbers are 3 and 2 (3 + 2 = 5 and 3 * 2 = 6).
-
Rewrite the middle term: Rewrite the middle term (5x) as the sum of the two numbers we found, 3x and 2x. Our expression now becomes: 6x² + 3x + 2x + 1.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
3x(2x + 1) + 1(2x + 1)
-
Factor out the common binomial: Notice that (2x + 1) is common to both terms. Factor it out:
(2x + 1)(3x + 1)
Therefore, the factored form of 6x² + 5x + 1 is (2x + 1)(3x + 1).
Method 2: Trial and Error
This method involves systematically testing different combinations of binomial factors until you find the correct pair. It's more intuitive but can be time-consuming for complex quadratics.
Steps:
-
Consider the factors of the leading coefficient (a): The factors of 6 are 1, 2, 3, and 6.
-
Consider the factors of the constant term (c): The factors of 1 are only 1 and 1.
-
Test combinations: We need to find combinations of factors that, when multiplied using the FOIL method (First, Outer, Inner, Last), result in the original expression. Let's try some combinations:
- (1x + 1)(6x + 1): Expanding this gives 6x² + 7x + 1 (Incorrect)
- (2x + 1)(3x + 1): Expanding this gives 6x² + 5x + 1 (Correct!)
This confirms that (2x + 1)(3x + 1) is the correct factorization.
Method 3: Using the Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can help find the roots of the quadratic equation 6x² + 5x + 1 = 0. These roots can then be used to determine the factors.
Steps:
-
Apply the quadratic formula: The quadratic formula states that for an equation ax² + bx + c = 0, the roots are given by:
x = (-b ± √(b² - 4ac)) / 2a
For our equation, a = 6, b = 5, and c = 1. Substituting these values, we get:
x = (-5 ± √(5² - 4 * 6 * 1)) / (2 * 6) x = (-5 ± √1) / 12 x₁ = (-5 + 1) / 12 = -4/12 = -1/3 x₂ = (-5 - 1) / 12 = -6/12 = -1/2
-
Convert roots to factors: If x₁ is a root, then (x - x₁) is a factor. Similarly, if x₂ is a root, then (x - x₂) is a factor. Therefore, our factors are:
(x + 1/3) and (x + 1/2)
-
Eliminate fractions: To obtain the same factors as in the previous methods, we can multiply each factor by 3 and 2 respectively to eliminate the fractions:
3(x + 1/3) = 3x + 1 2(x + 1/2) = 2x + 1
Thus, the factored form is (3x + 1)(2x + 1), which is consistent with our previous results.
A Deeper Look: The Discriminant
The expression inside the square root in the quadratic formula (b² - 4ac) is called the discriminant. It provides valuable information about the nature of the roots and the factorability of the quadratic expression:
-
If the discriminant is positive (b² - 4ac > 0): The quadratic equation has two distinct real roots, and the quadratic expression can be factored into two distinct linear binomials with real coefficients. This is the case with our example (6x² + 5x + 1), where the discriminant is 1.
-
If the discriminant is zero (b² - 4ac = 0): The quadratic equation has one repeated real root, and the quadratic expression is a perfect square trinomial.
-
If the discriminant is negative (b² - 4ac < 0): The quadratic equation has two complex conjugate roots, and the quadratic expression cannot be factored into linear binomials with real coefficients.
Why Factoring is Important
Factoring quadratic expressions is a fundamental skill in algebra with far-reaching applications:
-
Solving Quadratic Equations: Factoring allows us to solve quadratic equations by setting each factor equal to zero and solving for x. This is often simpler than using the quadratic formula, especially for easily factorable expressions.
-
Simplifying Algebraic Expressions: Factoring can simplify complex algebraic expressions, making them easier to manipulate and understand.
-
Graphing Parabolas: The factored form of a quadratic expression reveals the x-intercepts (roots) of the corresponding parabola, which is crucial for graphing the quadratic function.
-
Calculus Applications: Factoring is essential in calculus for techniques such as partial fraction decomposition and finding limits.
Frequently Asked Questions (FAQs)
Q: What if the quadratic expression cannot be factored easily?
A: If the quadratic expression cannot be easily factored using the methods described above, you can always use the quadratic formula to find the roots and then construct the factors. Alternatively, numerical methods can be employed to approximate the roots.
Q: Is there only one way to factor a quadratic expression?
A: No, the order of the factors doesn't matter. (2x + 1)(3x + 1) is the same as (3x + 1)(2x + 1).
Q: What happens if 'a' is negative?
A: If 'a' is negative, it's generally recommended to factor out -1 first to make the leading coefficient positive, simplifying the factoring process.
Q: Can all quadratic expressions be factored using real numbers?
A: No, as mentioned earlier, if the discriminant is negative, the quadratic expression cannot be factored into linear binomials with real coefficients.
Conclusion
Factoring the quadratic expression 6x² + 5x + 1, as demonstrated through three different methods, illustrates the versatility and importance of this algebraic technique. Understanding these methods empowers you to tackle a wide range of quadratic expressions and opens doors to more advanced mathematical concepts. Practice is key to mastering these techniques; try factoring other quadratic expressions to solidify your understanding and build confidence in your algebraic skills. Remember to always check your work by expanding the factored expression to ensure it matches the original quadratic. This process of verification is crucial for ensuring accuracy in your mathematical solutions.
Latest Posts
Latest Posts
-
Calcium Hydroxide Strong Or Weak
Sep 14, 2025
-
Where Is Mediterranean Agriculture Practiced
Sep 14, 2025
-
Objects That Sink In Water
Sep 14, 2025
-
What Is 2 Of 50
Sep 14, 2025
-
Is Burning A Physical Change
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Factor 6x 2 5x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.