Factor 6x 2 13x 6
thesills
Sep 15, 2025 · 5 min read
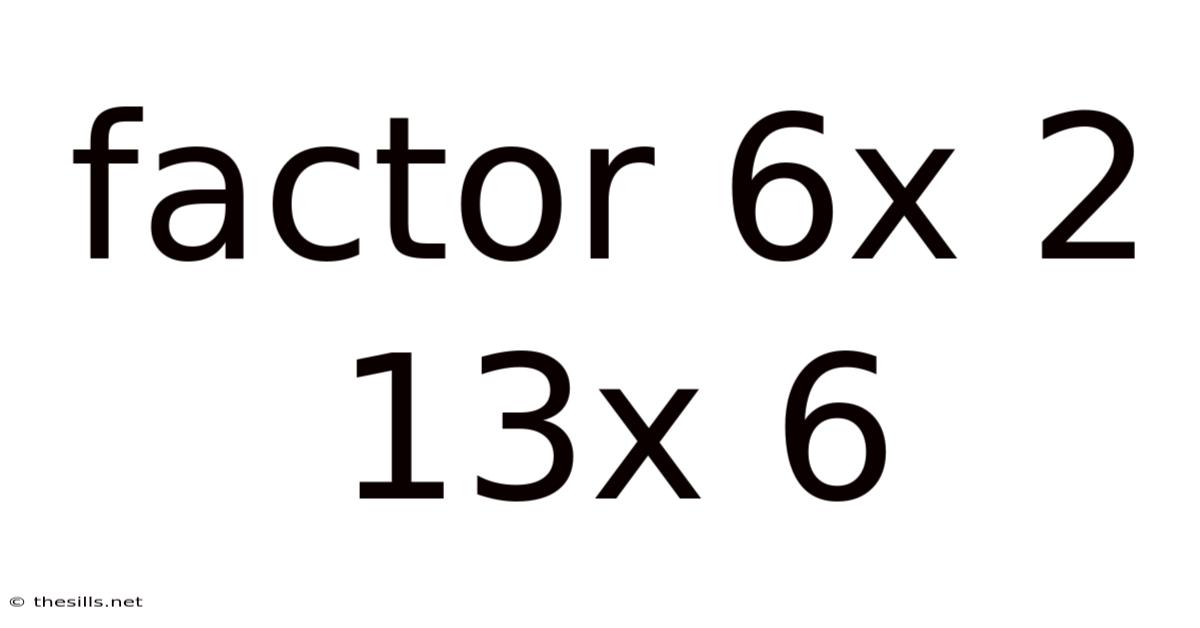
Table of Contents
Factoring the Quadratic Expression 6x² + 13x + 6: A Comprehensive Guide
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor these expressions efficiently and accurately is crucial for solving quadratic equations, simplifying algebraic fractions, and mastering more advanced mathematical concepts. This article provides a comprehensive guide to factoring the quadratic expression 6x² + 13x + 6, explaining the process step-by-step, exploring different methods, and addressing common questions. We'll delve into the underlying principles and provide practical examples to solidify your understanding.
Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic expression is ax² + bx + c, where a, b, and c are constants. In our case, the quadratic expression is 6x² + 13x + 6, where a = 6, b = 13, and c = 6. Factoring this expression means rewriting it as a product of two simpler expressions, usually two binomials.
Method 1: The AC Method (Splitting the Middle Term)
The AC method is a widely used technique for factoring quadratic expressions. It involves finding two numbers that add up to b (the coefficient of x) and multiply to ac (the product of the coefficients of x² and the constant term).
Steps:
-
Find the product ac: In our example, a = 6 and c = 6, so ac = 6 * 6 = 36.
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 13 (our b) and multiply to 36. These numbers are 9 and 4 (9 + 4 = 13 and 9 * 4 = 36).
-
Rewrite the middle term: Rewrite the middle term (13x) as the sum of the two numbers we found, multiplied by x. This gives us 6x² + 9x + 4x + 6.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
3x(2x + 3) + 2(2x + 3)
-
Factor out the common binomial: Notice that both terms now share the binomial (2x + 3). Factor this out:
(2x + 3)(3x + 2)
Therefore, the factored form of 6x² + 13x + 6 is (2x + 3)(3x + 2).
Method 2: Trial and Error
This method involves systematically trying different combinations of binomial factors until you find the correct one. It relies on understanding how binomial multiplication works.
Steps:
-
Consider the factors of the leading coefficient (a) and the constant term (c): The factors of 6 are (1, 6) and (2, 3). The factors of 6 are also (1, 6) and (2, 3).
-
Test different combinations: We need to find combinations that, when multiplied using the FOIL method (First, Outer, Inner, Last), result in the original expression. Let's try some combinations:
- (x + 1)(6x + 6): This expands to 6x² + 12x + 6, which is incorrect.
- (x + 2)(6x + 3): This expands to 6x² + 15x + 6, which is incorrect.
- (2x + 1)(3x + 6): This expands to 6x² + 15x + 6, which is incorrect.
- (2x + 3)(3x + 2): This expands to 6x² + 9x + 6x + 6 = 6x² + 13x + 6. This is correct!
Therefore, the factored form is again (2x + 3)(3x + 2). Note that the order of the factors doesn't matter; (3x + 2)(2x + 3) is also correct.
Method 3: Using the Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can help find the roots of the quadratic equation 6x² + 13x + 6 = 0. These roots can then be used to determine the factors.
The quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Substituting our values (a = 6, b = 13, c = 6):
x = [-13 ± √(13² - 4 * 6 * 6)] / (2 * 6) x = [-13 ± √(169 - 144)] / 12 x = [-13 ± √25] / 12 x = [-13 ± 5] / 12
This gives us two solutions:
x₁ = (-13 + 5) / 12 = -8 / 12 = -2/3 x₂ = (-13 - 5) / 12 = -18 / 12 = -3/2
The factors are then (x + 2/3) and (x + 3/2). To eliminate fractions, we multiply each factor by the denominator of the fraction:
(3x + 2) and (2x + 3)
This confirms our previous results: the factored form is (2x + 3)(3x + 2).
Explanation of the Underlying Principles
The success of these methods hinges on the distributive property (also known as the FOIL method) and the concept of finding common factors. When you multiply two binomials, (ax + b)(cx + d), you get: acx² + (ad + bc)x + bd. Factoring reverses this process. We're essentially working backward to find the original binomials that, when multiplied, produce the given quadratic expression.
Frequently Asked Questions (FAQ)
-
Q: What if the quadratic expression cannot be factored easily? A: Some quadratic expressions are not factorable using integer coefficients. In such cases, you can use the quadratic formula to find the roots and express the quadratic as a product of factors with potentially irrational or complex numbers.
-
Q: Is there only one correct way to factor a quadratic expression? A: No, the order of the factors doesn't matter. (2x + 3)(3x + 2) is equivalent to (3x + 2)(2x + 3).
-
Q: How can I check if my factoring is correct? A: Expand your factored expression using the FOIL method. If you get the original quadratic expression, your factoring is correct.
-
Q: What if the leading coefficient (a) is 1? A: Factoring becomes simpler. You only need to find two numbers that add up to b and multiply to c.
-
Q: What about factoring quadratic expressions with a negative leading coefficient? A: You can factor out -1 first to make the leading coefficient positive, making the factoring process easier. Then, factor the remaining expression using any of the methods described above.
Conclusion
Factoring the quadratic expression 6x² + 13x + 6 can be achieved using different methods, including the AC method, trial and error, and indirectly through the quadratic formula. Understanding these methods provides a versatile toolkit for solving quadratic equations and manipulating algebraic expressions. Mastering these techniques is essential for success in algebra and subsequent mathematical studies. Remember to practice regularly to develop fluency and accuracy in factoring quadratic expressions. The more you practice, the easier and faster it will become. Don’t be afraid to try different approaches and find the method that works best for you. Consistent practice and a thorough understanding of the underlying principles are key to success.
Latest Posts
Latest Posts
-
100g Glucose Equivalent In Food
Sep 15, 2025
-
First 5 Multiples Of 6
Sep 15, 2025
-
A Bond Dissociation Energy Is
Sep 15, 2025
-
Summation Of Odd Numbers Formula
Sep 15, 2025
-
Sf6 Hybridization Of Central Atom
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Factor 6x 2 13x 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.