Factor 4x 2 2x 1
thesills
Sep 12, 2025 · 6 min read
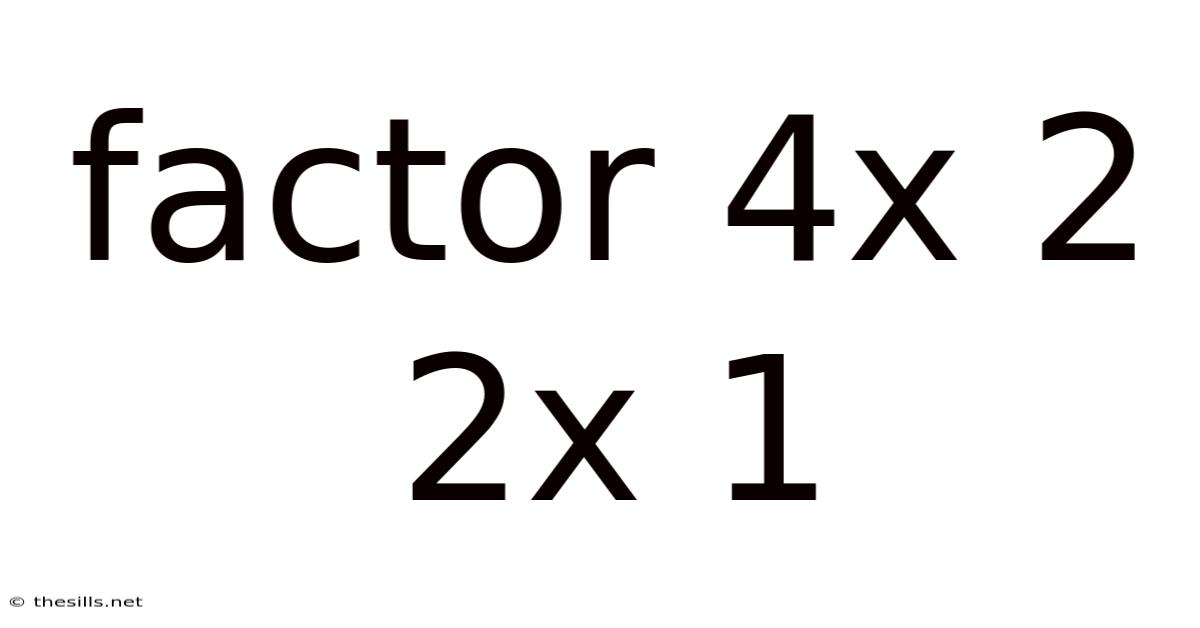
Table of Contents
Factoring the Quadratic Expression 4x² + 2x + 1: A Comprehensive Guide
Factoring quadratic expressions is a fundamental skill in algebra. It's a crucial step in solving quadratic equations, simplifying rational expressions, and understanding many other mathematical concepts. This article will delve into the process of factoring the specific quadratic expression 4x² + 2x + 1, exploring different methods and highlighting the underlying mathematical principles. We'll also address common misconceptions and provide a thorough explanation to help you master this important algebraic technique.
Understanding Quadratic Expressions
Before we tackle the factoring of 4x² + 2x + 1, let's review the basics of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a is not equal to zero. Our target expression, 4x² + 2x + 1, fits this standard form, with a = 4, b = 2, and c = 1.
The goal of factoring is to rewrite the quadratic expression as a product of two simpler expressions, usually linear binomials. This process reverses the multiplication process, allowing us to solve equations and simplify expressions more efficiently.
Attempting Traditional Factoring Methods
The most common factoring methods involve finding two numbers that add up to b and multiply to ac. However, let's see why this standard method doesn't directly work for 4x² + 2x + 1.
-
Finding factors of ac: In our case, a = 4 and c = 1, so ac = 4. The factors of 4 are (1, 4) and (2, 2).
-
Checking the sum: Neither pair (1 + 4 = 5) nor (2 + 2 = 4) adds up to b, which is 2. This indicates that the expression doesn't factor easily using this standard approach with integers.
This doesn't mean the expression is unfactorable. It simply means we need to explore other methods.
Exploring the Discriminant
The discriminant, denoted as Δ (delta), plays a crucial role in determining the nature of the roots of a quadratic equation and, by extension, the factorability of the quadratic expression. The discriminant is calculated using the formula:
Δ = b² - 4ac
For our expression, 4x² + 2x + 1:
Δ = (2)² - 4(4)(1) = 4 - 16 = -12
Since the discriminant is negative, this tells us several important things:
-
No Real Roots: The quadratic equation 4x² + 2x + 1 = 0 has no real roots. This means the parabola represented by the equation doesn't intersect the x-axis.
-
Complex Roots: The quadratic equation does have two complex roots (roots involving the imaginary unit i, where i² = -1).
-
Unfactorable with Real Numbers: The expression 4x² + 2x + 1 cannot be factored into two linear binomials with real coefficients.
Factoring with Complex Numbers
To factor 4x² + 2x + 1, we must utilize the quadratic formula, which provides the roots of a quadratic equation:
x = [-b ± √(b² - 4ac)] / 2a
Substituting the values from our expression:
x = [-2 ± √(-12)] / 8 = [-2 ± 2i√3] / 8 = [-1 ± i√3] / 4
These are the two complex roots of the quadratic equation. We can use these roots to express the factored form:
4x² + 2x + 1 = 4(x - [-1 + i√3]/4)(x - [-1 - i√3]/4)
This is the factored form of the expression using complex numbers. It’s important to understand that these factors involve complex numbers and are not as straightforward as those with real numbers.
Completing the Square Method
Another approach is completing the square. While this method doesn't lead to a simple factored form with real numbers, it offers valuable insights into the structure of the quadratic expression.
-
Divide by the coefficient of x²: Divide the entire expression by 4: x² + (1/2)x + (1/4)
-
Focus on the x and x² terms: We want to rewrite the expression in the form (x + p)² + q, where p and q are constants.
-
Find p: Take half of the coefficient of x: (1/2) / 2 = 1/4. This is our value for p.
-
Rewrite the expression: (x + 1/4)² Notice this expands to x² + (1/2)x + (1/16).
-
Adjust for the constant term: Our original expression had a constant term of 1/4. The completed square gives us 1/16. To balance, we need to add (1/4) - (1/16) = 3/16.
-
Final form: The completed square form is (x + 1/4)² + 3/16. This is not a factored form in the traditional sense, but it's a valuable equivalent representation.
Why Factoring is Important
Understanding factoring techniques, even when dealing with expressions that don't factor neatly with real numbers, is crucial for several reasons:
-
Solving Quadratic Equations: Factoring allows you to find the roots (solutions) of a quadratic equation by setting each factor to zero and solving for x. While our example has complex roots, this principle remains vital for equations with real roots.
-
Simplifying Rational Expressions: Factoring is essential for simplifying rational expressions (fractions with polynomials). By factoring both the numerator and denominator, you can often cancel common factors, leading to a simpler expression.
-
Graphing Quadratic Functions: The factored form of a quadratic expression reveals the x-intercepts of its graph (parabola). Although 4x² + 2x + 1 doesn't have real x-intercepts, factoring with real numbers in other quadratic functions directly shows where the parabola crosses the x-axis.
-
Advanced Mathematical Concepts: Factoring forms the foundation for many advanced mathematical concepts, including calculus, linear algebra, and abstract algebra.
Frequently Asked Questions (FAQ)
Q: Can all quadratic expressions be factored?
A: All quadratic expressions can be factored, but not always using real numbers. As we've seen, expressions with negative discriminants require complex numbers for complete factoring.
Q: Is there a shortcut to factor 4x² + 2x + 1?
A: There isn't a quick shortcut for this specific expression using only real numbers. The discriminant directly indicates that it doesn't factor easily using integer or rational coefficients. The most efficient approach is understanding why it doesn't factor traditionally and accepting its representation in terms of complex numbers or its completed square form.
Q: What if the discriminant is zero?
A: If the discriminant is zero, the quadratic equation has one repeated real root. The quadratic expression can be factored as a perfect square.
Q: Why is it important to know if an expression has complex roots?
A: Understanding whether roots are real or complex is crucial in various applications, such as in physics (oscillations), electrical engineering (AC circuits), and signal processing, where the nature of the roots determines the behavior of the system being modeled.
Conclusion
Factoring the quadratic expression 4x² + 2x + 1 presents a valuable opportunity to delve deeper into the intricacies of quadratic equations and factoring techniques. While the standard method fails to produce a simple factored form using real numbers, the negative discriminant clearly shows that the expression's roots are complex. Understanding the discriminant, employing the quadratic formula, and exploring completing the square provides a complete picture of how to work with and interpret this specific quadratic expression, strengthening your understanding of more complex algebraic concepts. The inability to factor this expression with real numbers is not a limitation; it opens the door to understanding complex numbers and expanding your algebraic toolkit. Mastering these concepts builds a solid foundation for more advanced mathematical studies.
Latest Posts
Latest Posts
-
Baking Soda Or Washing Soda
Sep 12, 2025
-
19th Letter Of The Alphabet
Sep 12, 2025
-
Energy Transformation Of A Lamp
Sep 12, 2025
-
Lewis Dot Symbol Of Mg
Sep 12, 2025
-
In The Ellipse Shown Below
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Factor 4x 2 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.