Factor 2x 2 9x 10
thesills
Sep 16, 2025 · 5 min read
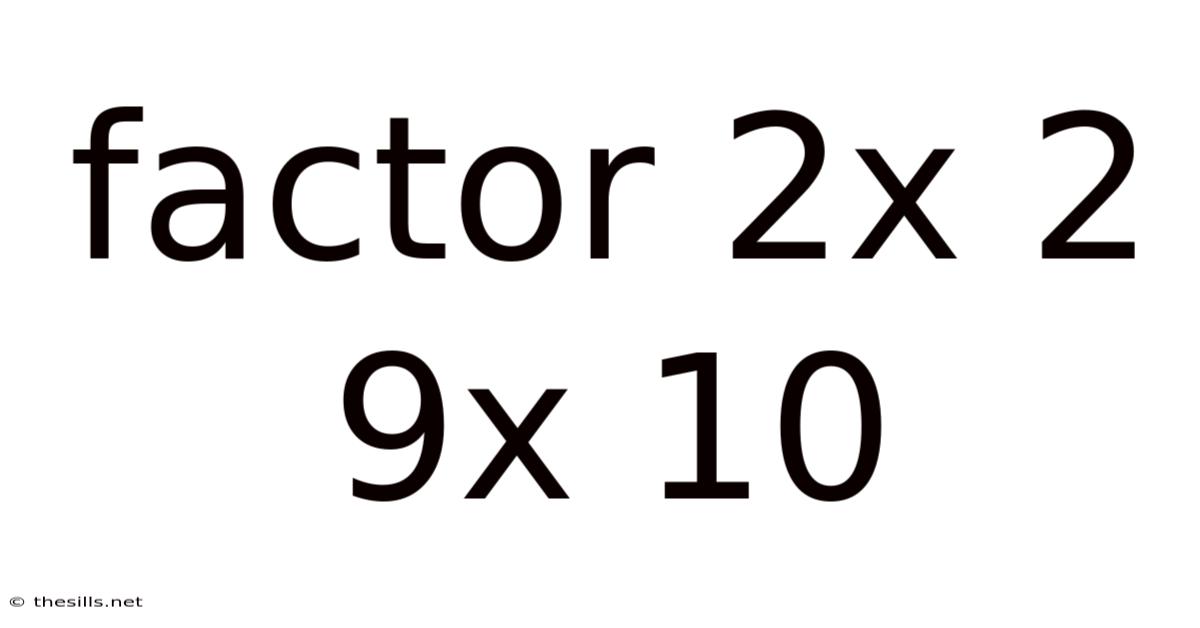
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 2x² + 9x + 10
This article provides a comprehensive guide to factoring the quadratic expression 2x² + 9x + 10. We'll explore various methods, explain the underlying mathematical principles, and delve into the practical applications of factoring. Understanding quadratic factoring is fundamental in algebra and crucial for solving a wide range of mathematical problems. By the end of this article, you'll not only be able to factor this specific expression but also gain the skills to tackle similar quadratic equations with confidence.
Introduction to Quadratic Expressions and Factoring
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. Factoring a quadratic expression involves rewriting it as a product of two simpler expressions, usually two binomials. This process is essential for solving quadratic equations, simplifying algebraic expressions, and understanding the behavior of parabolic curves (graphs of quadratic functions). Our focus here is on factoring 2x² + 9x + 10.
Method 1: AC Method (Product-Sum Method)
This is a widely used technique for factoring quadratic expressions. The steps are as follows:
-
Identify a, b, and c: In our expression, 2x² + 9x + 10, we have a = 2, b = 9, and c = 10.
-
Find the product ac: The product ac is 2 * 10 = 20.
-
Find two numbers that add up to b and multiply to ac: We need two numbers that add up to 9 (our 'b' value) and multiply to 20 (our 'ac' value). These numbers are 4 and 5 (4 + 5 = 9 and 4 * 5 = 20).
-
Rewrite the middle term: Rewrite the middle term (9x) using the two numbers we found: 2x² + 4x + 5x + 10.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
2x(x + 2) + 5(x + 2)
-
Factor out the common binomial: Notice that (x + 2) is a common factor in both terms. Factor it out:
(x + 2)(2x + 5)
Therefore, the factored form of 2x² + 9x + 10 is (x + 2)(2x + 5).
Method 2: Trial and Error
This method involves systematically trying different combinations of binomial factors until you find the one that works. It's less systematic than the AC method but can be faster with practice.
-
Consider the factors of the leading coefficient (a) and the constant term (c): The factors of 2 are 1 and 2. The factors of 10 are 1 and 10, and 2 and 5.
-
Set up binomial factors: We know the factors will be in the form (Ax + B)(Cx + D), where A and C are factors of 2, and B and D are factors of 10.
-
Test combinations: Let's try some combinations:
- (x + 1)(2x + 10): Expanding this gives 2x² + 12x + 10, which is incorrect.
- (x + 2)(2x + 5): Expanding this gives 2x² + 9x + 10, which is correct!
Therefore, the factored form is again (x + 2)(2x + 5).
Method 3: Quadratic Formula (Indirect Factoring)
While not a direct factoring method, the quadratic formula can help find the roots of the quadratic equation 2x² + 9x + 10 = 0, which can then be used to determine the factors.
The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a
Plugging in our values (a = 2, b = 9, c = 10), we get:
x = [-9 ± √(9² - 4 * 2 * 10)] / (2 * 2) x = [-9 ± √(81 - 80)] / 4 x = [-9 ± 1] / 4
This gives us two solutions: x = -2 and x = -5/2.
These solutions represent the roots of the equation. To find the factors, we can rewrite them as (x + 2) and (x + 5/2). To get rid of the fraction, we multiply the second factor by 2: (2x + 5). Thus, the factored form is (x + 2)(2x + 5).
Understanding the Significance of Factoring
Factoring quadratic expressions is not just a mathematical exercise. It has several important applications:
-
Solving Quadratic Equations: Setting the factored expression equal to zero allows us to easily solve the corresponding quadratic equation. For example, (x + 2)(2x + 5) = 0 implies x = -2 or x = -5/2.
-
Graphing Quadratic Functions: The factored form helps determine the x-intercepts (roots) of the parabola representing the quadratic function, providing key information about its shape and position on the coordinate plane.
-
Simplifying Algebraic Expressions: Factoring can simplify complex algebraic expressions by reducing them to a more manageable form.
-
Further Algebraic Manipulations: Factored forms are crucial in advanced algebraic operations such as partial fraction decomposition and solving systems of equations.
Frequently Asked Questions (FAQ)
-
What if the quadratic expression cannot be factored easily? If the expression cannot be factored using the methods described above (meaning there are no rational roots), the quadratic formula is always applicable. The roots obtained might be irrational or complex numbers.
-
Are there other methods for factoring quadratics? Yes, there are other specialized techniques, but the AC method and trial and error are the most commonly used for general quadratics.
-
Why is factoring important in higher-level mathematics? Factoring forms the basis of many advanced algebraic concepts and techniques, including calculus and linear algebra. It's a fundamental skill that extends beyond elementary algebra.
-
Can I use a calculator or software to factor quadratics? Yes, many calculators and mathematical software packages have built-in functions to factor polynomials. However, understanding the underlying methods is essential for developing problem-solving skills and deepening your understanding of algebra.
Conclusion
Factoring the quadratic expression 2x² + 9x + 10, resulting in (x + 2)(2x + 5), demonstrates a fundamental algebraic skill applicable in numerous contexts. We explored three different methods – the AC method, trial and error, and the indirect use of the quadratic formula – each offering a unique approach to solving the problem. Mastering these methods will significantly enhance your ability to solve quadratic equations, simplify expressions, and tackle more advanced mathematical problems in the future. The process of factoring is more than just finding the answer; it's about building a deeper understanding of the mathematical relationships between different algebraic expressions. Remember to practice regularly to improve your fluency and confidence in factoring quadratic expressions.
Latest Posts
Latest Posts
-
Large Unit Of Heat Energy
Sep 16, 2025
-
Lewis Dot Structure For Sicl4
Sep 16, 2025
-
Hclo Weak Or Strong Acid
Sep 16, 2025
-
During Photosynthesis Plants Take In
Sep 16, 2025
-
37 Deg C To F
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 9x 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.