Factor 2x 2 7x 3
thesills
Sep 15, 2025 · 6 min read
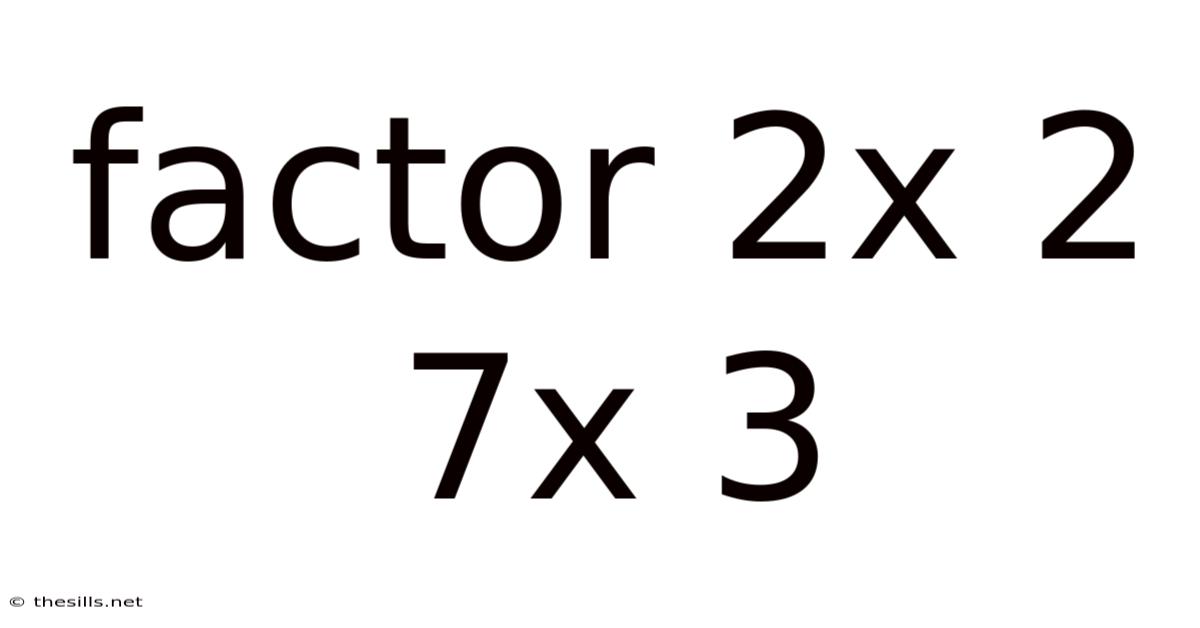
Table of Contents
Factoring the Quadratic Expression 2x² + 7x + 3: A Comprehensive Guide
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor allows you to solve quadratic equations, simplify complex expressions, and grasp more advanced mathematical concepts. This comprehensive guide will delve into the process of factoring the specific quadratic expression 2x² + 7x + 3, explaining the steps involved, the underlying mathematical principles, and offering strategies for tackling similar problems. We will explore different methods, ensuring you gain a thorough understanding of this important algebraic technique.
Understanding Quadratic Expressions
Before we jump into factoring 2x² + 7x + 3, let's refresh our understanding of quadratic expressions. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants (numbers). In our case, a = 2, b = 7, and c = 3.
Factoring a quadratic expression means rewriting it as a product of two simpler expressions, usually two binomials. This process is the reverse of expanding binomials using the distributive property (often remembered by the acronym FOIL: First, Outer, Inner, Last).
Method 1: AC Method (Product-Sum Method)
The AC method is a widely used technique for factoring quadratic expressions. It's particularly helpful when the coefficient of x² (the 'a' term) is not equal to 1. Here's how it works for 2x² + 7x + 3:
-
Find the product 'ac': Multiply the coefficient of x² (a = 2) by the constant term (c = 3). This gives us ac = 2 * 3 = 6.
-
Find two numbers that add up to 'b' and multiply to 'ac': We need to find two numbers that add up to 7 (the coefficient of x, which is 'b') and multiply to 6 (which is 'ac'). These numbers are 6 and 1 (6 + 1 = 7 and 6 * 1 = 6).
-
Rewrite the middle term: Rewrite the middle term (7x) as the sum of the two numbers we found, using x as the variable. This gives us 6x + 1x, or simply 6x + x.
-
Factor by grouping: Rewrite the original quadratic expression, replacing 7x with 6x + x: 2x² + 6x + x + 3. Now, group the terms in pairs: (2x² + 6x) + (x + 3).
-
Factor out common factors: Factor out the greatest common factor (GCF) from each pair of terms. From (2x² + 6x), we can factor out 2x, leaving us with 2x(x + 3). From (x + 3), the GCF is 1, so we have 1(x + 3).
-
Factor out the common binomial: Now we have 2x(x + 3) + 1(x + 3). Notice that (x + 3) is a common factor in both terms. We can factor it out: (x + 3)(2x + 1).
Therefore, the factored form of 2x² + 7x + 3 is (x + 3)(2x + 1).
Method 2: Trial and Error
The trial and error method involves directly guessing the binomial factors. While it can be quicker for some, it requires practice and intuition. Here's how it works for 2x² + 7x + 3:
-
Consider the factors of the 'a' term: The coefficient of x² is 2, which has factors 1 and 2. These will be the coefficients of x in our binomials.
-
Consider the factors of the 'c' term: The constant term is 3, which has factors 1 and 3. These will be the constant terms in our binomials.
-
Test different combinations: We need to find a combination that, when expanded using FOIL, gives us the original quadratic expression. Let's try some possibilities:
- (x + 1)(2x + 3): Expanding this gives 2x² + 5x + 3 (incorrect).
- (x + 3)(2x + 1): Expanding this gives 2x² + 7x + 3 (correct!).
Therefore, the factored form is again (x + 3)(2x + 1).
Understanding the Underlying Mathematics
The success of both methods hinges on the distributive property and the fundamental theorem of algebra. The distributive property (a(b + c) = ab + ac) allows us to expand binomials, while the fundamental theorem of algebra states that a polynomial of degree n has exactly n roots (or solutions) in the complex number system. For a quadratic (degree 2), this means there are two roots. Factoring helps us find these roots.
When we factor 2x² + 7x + 3 into (x + 3)(2x + 1), we've essentially found the roots of the corresponding quadratic equation 2x² + 7x + 3 = 0. Setting each factor to zero gives us the solutions: x + 3 = 0 (x = -3) and 2x + 1 = 0 (x = -1/2). These are the x-intercepts of the parabola representing the quadratic function.
Solving Quadratic Equations using Factoring
Once you've factored a quadratic expression, you can readily solve the corresponding quadratic equation. Let's illustrate with our example:
The equation is 2x² + 7x + 3 = 0. We've already factored it as (x + 3)(2x + 1) = 0. The zero product property states that if the product of two factors is zero, then at least one of the factors must be zero. Therefore:
- x + 3 = 0 => x = -3
- 2x + 1 = 0 => 2x = -1 => x = -1/2
So, the solutions to the equation 2x² + 7x + 3 = 0 are x = -3 and x = -1/2.
Expanding our Understanding: Different Types of Quadratic Expressions
Not all quadratic expressions are easily factored using these methods. Some may involve irrational or complex roots. Others may not factor at all using integer coefficients. In such cases, other techniques like the quadratic formula are necessary. However, mastering the factoring of simpler quadratics like 2x² + 7x + 3 provides a solid foundation for tackling more complex scenarios.
Frequently Asked Questions (FAQ)
-
Q: What if the 'a' term is 1? A: If a = 1, the factoring process simplifies. You only need to find two numbers that add up to 'b' and multiply to 'c'. For example, factoring x² + 5x + 6 would involve finding two numbers that add to 5 and multiply to 6 (these are 2 and 3), leading to the factored form (x + 2)(x + 3).
-
Q: What if the quadratic expression is not factorable using integers? A: In such cases, you can use the quadratic formula, which always provides solutions (though they may be irrational or complex numbers). The quadratic formula is: x = [-b ± √(b² - 4ac)] / 2a.
-
Q: Can I check my factored answer? A: Yes, always expand your factored answer using the FOIL method to verify if it matches the original quadratic expression. This is a crucial step to ensure accuracy.
-
Q: Why is factoring important? A: Factoring is a crucial skill in algebra because it allows you to solve quadratic equations, simplify algebraic expressions, and understand the behavior of quadratic functions (parabolas). It's a building block for more advanced mathematical concepts.
Conclusion
Factoring the quadratic expression 2x² + 7x + 3, whether using the AC method or trial and error, provides valuable practice in a fundamental algebraic technique. Understanding the underlying mathematical principles and practicing different methods will build your confidence and skills in solving quadratic equations and manipulating algebraic expressions. Remember to always check your work by expanding your factored answer. Mastering this skill will significantly enhance your understanding of algebra and pave the way for success in more advanced mathematical studies. Practice consistently, and you'll soon find factoring quadratic expressions becomes second nature.
Latest Posts
Latest Posts
-
Molecular Orbital Diagram O2 2
Sep 15, 2025
-
Single Celled Organism Is Called
Sep 15, 2025
-
Study Of Sound Mechanical Waves
Sep 15, 2025
-
Rectangular Prism With 5 Cubes
Sep 15, 2025
-
How To Find Work Function
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about Factor 2x 2 7x 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.