Derivative Of 1 2x 1
thesills
Sep 14, 2025 · 5 min read
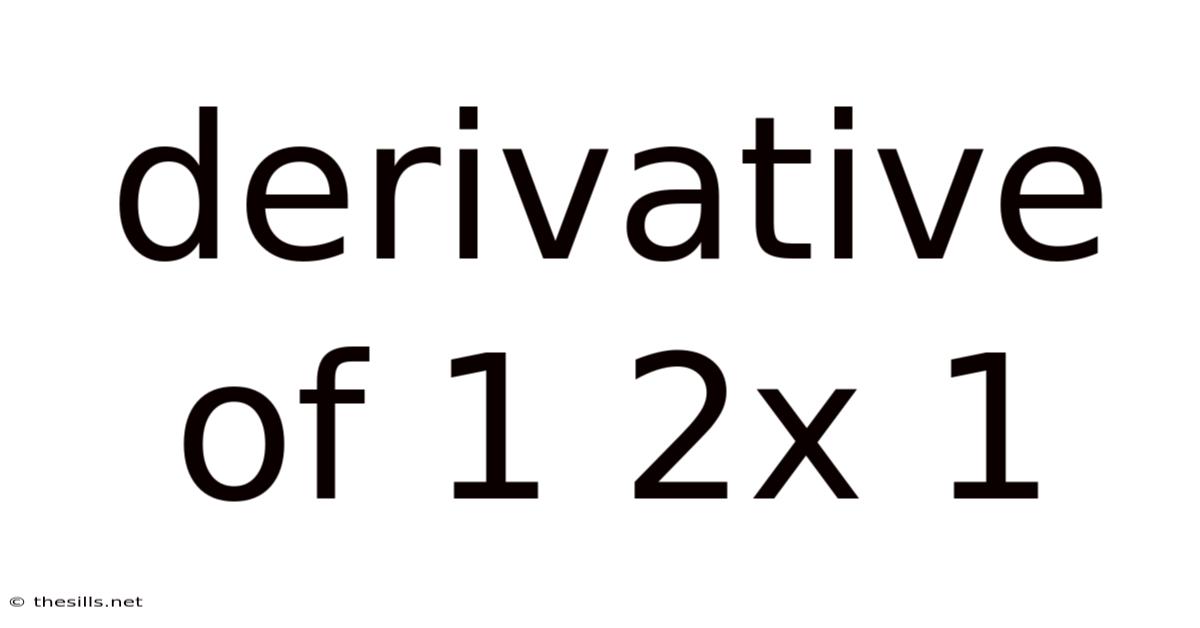
Table of Contents
Understanding the Derivative of 1/(2x + 1): A Comprehensive Guide
Finding the derivative of a function is a cornerstone of calculus, allowing us to analyze rates of change and slopes of curves. This article provides a comprehensive explanation of how to find the derivative of the function f(x) = 1/(2x + 1), covering the underlying principles, step-by-step calculations, and addressing common questions. We will explore different approaches, emphasizing a deep understanding rather than rote memorization. This guide is suitable for students learning calculus, as well as anyone seeking a refresher on differentiation techniques.
Introduction: The Power of Derivatives
The derivative of a function, denoted as f'(x) or df/dx, represents the instantaneous rate of change of the function at any given point. Geometrically, it corresponds to the slope of the tangent line to the function's graph at that point. Understanding derivatives is crucial in various fields, from physics (analyzing velocity and acceleration) to economics (modeling growth and decay). The function we're focusing on, 1/(2x + 1), presents a good opportunity to practice using several important derivative rules.
Method 1: Using the Quotient Rule
The quotient rule is a powerful tool for differentiating functions expressed as fractions. If we have a function of the form f(x) = g(x) / h(x), then its derivative is given by:
f'(x) = [h(x)g'(x) - g(x)h'(x)] / [h(x)]²
In our case, g(x) = 1 and h(x) = (2x + 1). Therefore:
- g'(x) = d(1)/dx = 0 (the derivative of a constant is always zero)
- h'(x) = d(2x + 1)/dx = 2 (the derivative of 2x is 2, and the derivative of 1 is 0)
Applying the quotient rule:
f'(x) = [(2x + 1)(0) - (1)(2)] / (2x + 1)² f'(x) = -2 / (2x + 1)²
Method 2: Using the Chain Rule and Power Rule
We can rewrite the function as f(x) = (2x + 1)^-1. This allows us to apply the chain rule, which states that the derivative of a composite function is the derivative of the outer function (with the inside function left alone) times the derivative of the inside function. Combined with the power rule (d/dx(xⁿ) = nxⁿ⁻¹), we get:
-
Power Rule: The derivative of (2x + 1)^-1 is -1(2x + 1)^-2.
-
Chain Rule: We need to multiply this by the derivative of the inside function (2x + 1), which is 2.
Therefore:
f'(x) = -1(2x + 1)^-2 * 2 f'(x) = -2(2x + 1)^-2 f'(x) = -2 / (2x + 1)²
This confirms the result we obtained using the quotient rule. Both methods lead to the same derivative.
Understanding the Result: Interpretation and Implications
The derivative we found, f'(x) = -2 / (2x + 1)², provides valuable information about the original function, f(x) = 1/(2x + 1).
-
Slope of the Tangent: At any point x, f'(x) gives the slope of the tangent line to the graph of f(x). Notice that the derivative is always negative, except when the denominator is undefined (at x = -1/2). This indicates that the function is always decreasing where it's defined.
-
Rate of Change: The derivative describes the instantaneous rate of change of f(x). The magnitude of the derivative indicates the steepness of the curve. As x moves further away from -1/2, the magnitude of the derivative decreases, meaning the curve becomes less steep.
-
Critical Points: The derivative is never equal to zero, meaning there are no critical points (local maxima or minima) for the function 1/(2x + 1).
-
Asymptotes: The function has a vertical asymptote at x = -1/2, where the denominator becomes zero. The derivative also approaches infinity as x approaches -1/2, reflecting the infinite slope at the asymptote.
Further Exploration: Higher-Order Derivatives
We can find higher-order derivatives by repeatedly differentiating the function. For example:
- Second Derivative: To find the second derivative (f''(x)), we differentiate f'(x) = -2(2x + 1)^-2. Using the chain rule and power rule again:
f''(x) = 8(2x + 1)^-3 = 8 / (2x + 1)³
- Third Derivative: Differentiating f''(x) will give us the third derivative, and so on.
Frequently Asked Questions (FAQ)
Q1: What if the numerator was not a constant?
If the numerator was a function of x, you would still use the quotient rule or, after rewriting the expression, the chain rule and power rule. The process would be slightly more complex, involving the derivative of the numerator as well.
Q2: Why is the derivative always negative?
The negative sign in the derivative (-2/(2x+1)²) arises from the power rule applied to (2x+1)^-1. The negative exponent indicates an inversely proportional relationship. As x increases, the function's value decreases, leading to a negative derivative.
Q3: What does it mean when the derivative is undefined?
The derivative is undefined at x = -1/2 because the denominator (2x + 1)² becomes zero. This corresponds to a vertical asymptote in the graph of the original function. The slope of the tangent line at this point is considered infinite.
Q4: How can I check my answer?
You can use online derivative calculators or graphing tools to verify your calculations. These tools can compute derivatives and visually represent the function and its derivative, providing a visual confirmation of your work. However, understanding the underlying method is crucial for problem-solving.
Conclusion: Mastering Differentiation Techniques
This comprehensive guide demonstrated multiple approaches to finding the derivative of 1/(2x + 1). We highlighted the application of the quotient rule and the chain rule in conjunction with the power rule. Understanding these techniques is essential for anyone studying calculus. Remember that the derivative provides valuable insights into the behavior of a function, including its rate of change, slope of tangents, and critical points. By mastering these techniques and understanding their application, you develop a solid foundation in differential calculus and gain the ability to analyze and interpret a wide range of mathematical functions. Keep practicing, and you'll soon find yourself confidently navigating the world of derivatives!
Latest Posts
Latest Posts
-
Integral Form Of Gauss Law
Sep 14, 2025
-
1 Au In Light Years
Sep 14, 2025
-
Do Non Metals Gain Electrons
Sep 14, 2025
-
What Is 0 0098 Boiling Point
Sep 14, 2025
-
Sample Space For Two Dice
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of 1 2x 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.