7.5 As A Mixed Number
thesills
Sep 15, 2025 · 6 min read
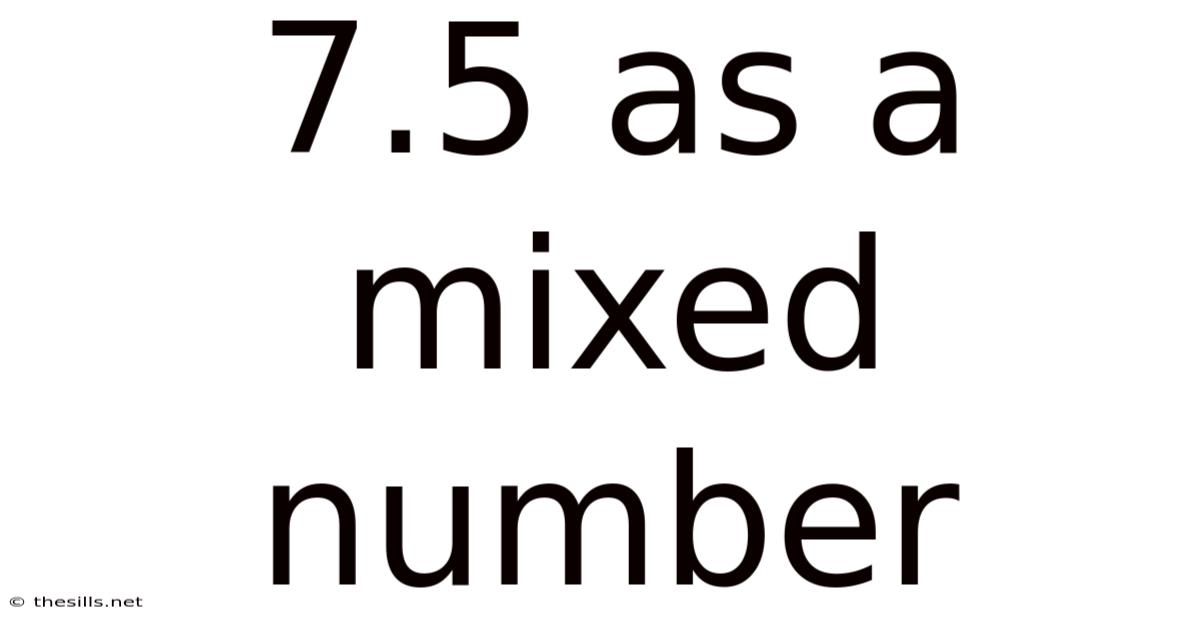
Table of Contents
Understanding 7.5 as a Mixed Number: A Comprehensive Guide
Many of us encounter decimal numbers like 7.5 in everyday life, from measuring ingredients in a recipe to calculating our finances. But what does 7.5 actually mean, and how can we represent it in different ways? This comprehensive guide will explore the concept of 7.5 as a mixed number, breaking down the process step-by-step and providing a deeper understanding of fractional representation. We'll also delve into the underlying mathematical principles and address frequently asked questions.
Introduction to Mixed Numbers and Improper Fractions
Before diving into 7.5, let's clarify some fundamental concepts. A mixed number combines a whole number and a proper fraction. For example, 2 ¾ is a mixed number; it represents two whole units and three-quarters of another unit. An improper fraction, on the other hand, has a numerator (top number) that is greater than or equal to its denominator (bottom number). For instance, 11/4 is an improper fraction because the numerator (11) is larger than the denominator (4). Both mixed numbers and improper fractions represent the same value; they are simply different ways of expressing the same quantity. Converting between these forms is a crucial skill in mathematics.
Converting 7.5 to a Mixed Number: A Step-by-Step Approach
The decimal number 7.5 represents seven whole units and five-tenths of another unit. To convert this to a mixed number, we need to focus on the fractional part – the ".5".
Step 1: Identify the Fractional Part
The decimal 0.5 represents the fractional portion of our number.
Step 2: Convert the Decimal to a Fraction
The decimal 0.5 can be written as the fraction 5/10. This is because the "5" is in the tenths place.
Step 3: Simplify the Fraction (Reduce to Lowest Terms)
The fraction 5/10 can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 5 and 10 is 5. Dividing both the numerator and the denominator by 5, we get:
5/10 = 1/2
Step 4: Combine the Whole Number and the Simplified Fraction
Now, we combine the whole number part (7) with the simplified fraction (1/2) to obtain the mixed number:
7 ½
Therefore, 7.5 as a mixed number is 7 ½.
Understanding the Mathematical Principles
The conversion process hinges on the understanding of place value in the decimal system. Each digit to the right of the decimal point represents a fraction with a denominator that is a power of 10. The first digit after the decimal point is in the tenths place (1/10), the second is in the hundredths place (1/100), the third in the thousandths place (1/1000), and so on.
When we convert 0.5 to a fraction, we are essentially expressing the value of the digit "5" in its corresponding place value. The "5" is in the tenths place, hence it represents 5/10. Simplifying this fraction is a matter of reducing it to its lowest terms, finding the simplest equivalent fraction. This ensures that the fraction is expressed in its most concise form.
Converting Improper Fractions to Mixed Numbers (and Vice Versa)
It's important to understand the relationship between improper fractions and mixed numbers. While we've already converted a decimal to a mixed number, let's explore the reciprocal process. The improper fraction equivalent to 7 ½ is 15/2. This is because:
(7 * 2) + 1 = 15
The denominator remains the same (2). The numerator becomes the result of the calculation.
To convert an improper fraction like 15/2 back to a mixed number, we perform the opposite operation – division:
15 ÷ 2 = 7 with a remainder of 1.
The quotient (7) becomes the whole number part of the mixed number, and the remainder (1) becomes the numerator of the fraction, while the denominator remains the same (2). Thus, 15/2 = 7 ½.
Real-World Applications of Mixed Numbers
Understanding mixed numbers is essential in various real-world contexts. Here are a few examples:
- Cooking and Baking: Recipes often use mixed numbers to specify ingredient amounts, like 2 ½ cups of flour or 1 ¼ teaspoons of baking powder.
- Measurement: Many measurements, especially in construction or engineering, involve mixed numbers, such as 5 ¾ inches or 12 ½ feet.
- Time: Time is often expressed using mixed numbers; for example, 1 ½ hours or 2 ¾ minutes.
- Finance: Calculations involving money might include mixed numbers, such as 7 ½ dollars or 3 ¼ cents.
Beyond 7.5: Working with Other Decimal Numbers
The method described above can be applied to convert any decimal number to a mixed number. For instance:
- 3.75: The fractional part is 0.75 = 75/100 = 3/4. Therefore, 3.75 = 3 ¾.
- 12.2: The fractional part is 0.2 = 2/10 = 1/5. Therefore, 12.2 = 12 1/5.
- 0.625: The fractional part is 625/1000, which simplifies to 5/8. Therefore, 0.625 = 5/8 (this is already a proper fraction and not a mixed number).
Remember to always simplify the fraction to its lowest terms for the most accurate and concise representation.
Frequently Asked Questions (FAQ)
Q1: Why do we need to convert decimals to mixed numbers?
A1: While decimals are convenient for calculations, mixed numbers offer a more intuitive representation, especially when dealing with quantities that are not whole numbers. Mixed numbers clearly show the whole number component and the fractional part, making them easier to visualize and understand in many contexts.
Q2: Can all decimals be converted to mixed numbers?
A2: Not all decimals can be converted to mixed numbers. Decimals that are already less than 1 (like 0.75 or 0.625) will result in a proper fraction, not a mixed number. Only decimals greater than or equal to 1 can be expressed as mixed numbers.
Q3: What if the decimal has more than one digit after the decimal point?
A3: The same principle applies. For example, let's convert 2.375:
- 0.375 = 375/1000.
- Simplifying this fraction yields 3/8.
- Therefore, 2.375 = 2 3/8.
Q4: Is there a quicker way to convert decimals to fractions?
A4: While the step-by-step method is helpful for understanding the underlying principles, you can expedite the process with practice. For common decimal values like 0.5, 0.25, 0.75, and 0.125, you'll quickly memorize their fractional equivalents (1/2, 1/4, 3/4, and 1/8 respectively).
Q5: Why is simplifying fractions important?
A5: Simplifying fractions ensures accuracy and clarity. A simplified fraction represents the same value as the original fraction but in its most concise form. It makes calculations easier and prevents confusion.
Conclusion
Understanding the conversion of decimals, such as 7.5, into mixed numbers is a fundamental skill in mathematics with numerous practical applications. By mastering this conversion, you'll not only improve your mathematical proficiency but also enhance your ability to solve real-world problems involving measurements, quantities, and proportions. Remember to break down the process step-by-step, focus on place value, and always simplify your fractions to their lowest terms. This approach ensures accuracy and makes working with fractions much more manageable and intuitive. The seemingly simple task of converting 7.5 to 7 ½ opens the door to a deeper understanding of the interconnectedness of various mathematical concepts and their real-world significance.
Latest Posts
Latest Posts
-
Number Of Atoms In Na
Sep 15, 2025
-
1000 Liter To Meter Cube
Sep 15, 2025
-
What Flies In The Sky
Sep 15, 2025
-
Japan And The United Nations
Sep 15, 2025
-
Small Meaningful Gifts For Him
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 7.5 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.