6x2 + 11x + 3
thesills
Sep 18, 2025 · 5 min read
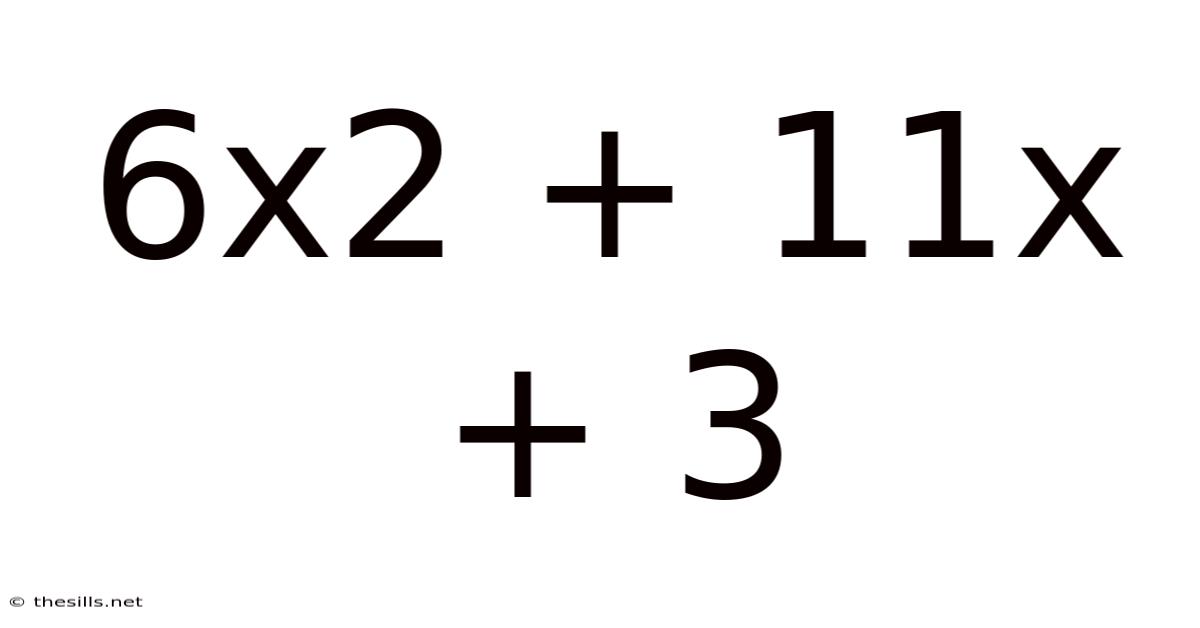
Table of Contents
Unveiling the Secrets of 6x² + 11x + 3: A Deep Dive into Quadratic Expressions
This article delves into the fascinating world of quadratic expressions, specifically focusing on the expression 6x² + 11x + 3. We'll explore various methods for factoring this expression, understand its graphical representation, and uncover its practical applications in mathematics and beyond. This comprehensive guide is perfect for students struggling with algebra, as well as anyone seeking a deeper understanding of quadratic equations. Understanding quadratic expressions like this one is fundamental to more advanced mathematical concepts.
Introduction to Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually 'x') is 2. It generally takes the form ax² + bx + c, where 'a', 'b', and 'c' are constants and 'a' is not equal to zero. Our focus, 6x² + 11x + 3, perfectly fits this mold, with a = 6, b = 11, and c = 3. Understanding how to manipulate and solve these types of expressions is crucial in various fields, from physics to computer science.
Method 1: Factoring by Grouping
This method involves splitting the middle term (11x) into two terms whose sum is 11x and whose product is equal to the product of the first and last terms (6x² * 3 = 18x²). Let's break down the process step-by-step:
-
Find the factors: We need two numbers that add up to 11 and multiply to 18. These numbers are 9 and 2.
-
Rewrite the middle term: Rewrite the expression as 6x² + 9x + 2x + 3.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
- 3x(2x + 3) + 1(2x + 3)
-
Factor out the common binomial: Notice that (2x + 3) is common to both terms. Factor it out:
- (2x + 3)(3x + 1)
Therefore, the factored form of 6x² + 11x + 3 is (2x + 3)(3x + 1).
Method 2: Using the Quadratic Formula
The quadratic formula provides a more general approach to solving quadratic equations, even when factoring by grouping proves difficult or impossible. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression, a = 6, b = 11, and c = 3. Substituting these values into the quadratic formula yields:
x = [-11 ± √(11² - 4 * 6 * 3)] / (2 * 6) x = [-11 ± √(121 - 72)] / 12 x = [-11 ± √49] / 12 x = [-11 ± 7] / 12
This gives us two possible solutions for x:
- x = (-11 + 7) / 12 = -4 / 12 = -1/3
- x = (-11 - 7) / 12 = -18 / 12 = -3/2
These solutions represent the x-intercepts (roots) of the quadratic equation 6x² + 11x + 3 = 0. Notice how these solutions relate to the factors we found earlier: if 2x + 3 = 0, then x = -3/2; and if 3x + 1 = 0, then x = -1/3.
Method 3: AC Method
The AC method is another useful technique for factoring quadratic trinomials. Here's how it works for 6x² + 11x + 3:
-
Find the product AC: Multiply the coefficient of the x² term (a) by the constant term (c): 6 * 3 = 18
-
Find two numbers: Find two numbers that add up to the coefficient of the x term (b) which is 11 and multiply to 18. These numbers are 9 and 2.
-
Rewrite the expression: Rewrite the middle term using these two numbers: 6x² + 9x + 2x + 3
-
Factor by grouping: This step is the same as in Method 1. Group the terms and factor out the GCF from each pair: 3x(2x + 3) + 1(2x + 3) = (2x + 3)(3x + 1)
The AC method provides a systematic approach to factoring, especially helpful when dealing with larger coefficients.
Graphical Representation
The graph of the quadratic equation y = 6x² + 11x + 3 is a parabola. The parabola opens upwards because the coefficient of the x² term (a = 6) is positive. The x-intercepts of the parabola are the solutions we found using the quadratic formula: x = -1/3 and x = -3/2. The y-intercept is found by setting x = 0, resulting in y = 3. The vertex of the parabola, the lowest point, can be calculated using the formula x = -b/2a, which gives x = -11/12. Substituting this value back into the equation gives the y-coordinate of the vertex.
Understanding the graphical representation helps visualize the behavior of the quadratic expression and its relationship to its roots and other key features.
Practical Applications
Quadratic expressions are not just abstract mathematical concepts; they have numerous real-world applications:
-
Physics: Projectile motion, where the height of an object over time follows a parabolic path, is often modeled using quadratic equations.
-
Engineering: Designing bridges, arches, and other structures frequently involves using quadratic equations to ensure stability and strength.
-
Economics: Quadratic functions can be used to model cost, revenue, and profit functions, helping businesses make informed decisions.
-
Computer graphics: Parabolas and other quadratic curves are frequently used in creating smooth, realistic curves in computer-generated images and animations.
Frequently Asked Questions (FAQ)
Q: What if I can't factor the quadratic expression easily?
A: If factoring by grouping or the AC method proves difficult, the quadratic formula is always a reliable alternative. It will provide the roots of the equation, even if they are irrational or complex numbers.
Q: What does it mean if the discriminant (b² - 4ac) is negative?
A: A negative discriminant indicates that the quadratic equation has no real roots. The parabola does not intersect the x-axis. The roots are complex numbers (involving the imaginary unit 'i').
Q: Are there other methods for solving quadratic equations?
A: Yes, completing the square is another technique that can be used to solve quadratic equations. It involves manipulating the equation to create a perfect square trinomial, which can then be easily factored.
Conclusion
Understanding quadratic expressions like 6x² + 11x + 3 is a fundamental skill in algebra and has broad applications across various disciplines. This article has explored multiple methods for factoring and solving this specific expression, along with its graphical representation and practical relevance. By mastering these techniques, you'll be well-equipped to tackle more complex mathematical problems and gain a deeper appreciation for the power and versatility of quadratic equations. Remember, practice is key! The more you work with these expressions, the more comfortable and confident you'll become. Don't hesitate to revisit these methods and try factoring other quadratic expressions to solidify your understanding.
Latest Posts
Latest Posts
-
Is 2 3 Irrational Or Rational
Sep 18, 2025
-
What Animals Can You Ride
Sep 18, 2025
-
First 6 Multiples Of 5
Sep 18, 2025
-
Balance The Equation Co Fe2o3 Fe Co2
Sep 18, 2025
-
Components Of The Respiratory Membrane
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about 6x2 + 11x + 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.