6x 2 X 2 0
thesills
Sep 17, 2025 · 6 min read
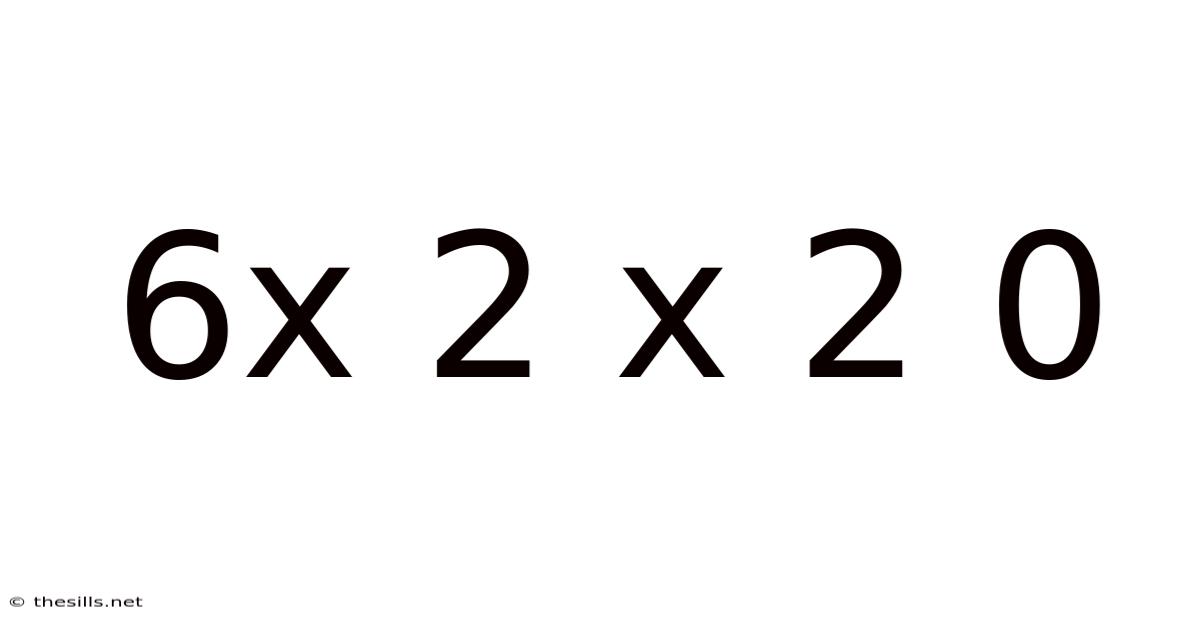
Table of Contents
Decoding 6x2x20: A Deep Dive into Number Sense, Mathematical Operations, and Problem-Solving
The seemingly simple sequence "6 x 2 x 20" presents a fascinating opportunity to explore several key mathematical concepts and problem-solving strategies. While the calculation itself is straightforward, analyzing its components allows us to delve into number sense, different approaches to multiplication, and the importance of understanding the order of operations. This article will unpack this seemingly simple expression, exploring its solution, discussing the underlying mathematical principles, and expanding on related concepts to enhance your mathematical understanding.
Understanding the Fundamentals: Multiplication and Order of Operations
At its core, "6 x 2 x 20" is a multiplication problem. Multiplication is a fundamental arithmetic operation representing repeated addition. In this case, we're repeatedly adding 6, 2 times, and then the result of that is repeatedly added 20 times. However, the order in which we perform these multiplications doesn't affect the final answer due to the commutative and associative properties of multiplication.
The commutative property states that the order of the numbers in a multiplication problem doesn't change the product (a x b = b x a). The associative property states that the grouping of numbers in a multiplication problem doesn't change the product ((a x b) x c = a x (b x c)). These properties are crucial for simplifying calculations and choosing efficient strategies.
The order of operations, often remembered by the acronym PEMDAS/BODMAS (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction), dictates the sequence in which operations should be performed. Since our expression contains only multiplication, the order doesn't strictly matter in this specific case.
Calculating 6 x 2 x 20: Different Approaches
Let's explore different ways to solve this problem, highlighting different mathematical approaches and strategies:
Method 1: Sequential Multiplication
This is the most straightforward method. We perform the multiplications step-by-step:
- 6 x 2 = 12
- 12 x 20 = 240
Therefore, 6 x 2 x 20 = 240.
Method 2: Commutative Property and Simplification
We can use the commutative property to rearrange the numbers for easier calculation:
- Rearrange: 2 x 20 x 6
- Calculate: 40 x 6 = 240
This method simplifies the calculation by first multiplying the smaller numbers, making the final multiplication less complex.
Method 3: Associative Property and Simplification
Similar to the previous method, but utilizing the associative property:
- Group: (6 x 2) x 20
- Calculate: 12 x 20 = 240
Or:
- Group: 6 x (2 x 20)
- Calculate: 6 x 40 = 240
This demonstrates the flexibility afforded by understanding the associative property. Choosing the grouping that simplifies the calculation is key to efficient problem-solving.
Method 4: Mental Math Techniques
For those proficient in mental math, the problem can be solved mentally using various techniques:
- Breaking down numbers: Think of 20 as 2 x 10. Then 6 x 2 x 2 x 10 becomes (6 x 2 x 2) x 10 = 24 x 10 = 240.
- Using known facts: Recognize that 6 x 20 is 120, and doubling 120 is 240.
These methods demonstrate that understanding number relationships and having a strong foundation in multiplication facts significantly speeds up the calculation process.
Expanding on the Concepts: Beyond the Calculation
While solving 6 x 2 x 20 is relatively simple, let’s expand on the underlying mathematical concepts to build a deeper understanding:
-
Factors and Multiples: The numbers 6, 2, and 20 are factors of 240. 240 is a multiple of 6, 2, and 20. Understanding factors and multiples is crucial in number theory and algebra.
-
Prime Factorization: Expressing numbers as a product of their prime factors is a powerful tool. The prime factorization of 240 is 2⁴ x 3 x 5. This provides valuable insights into the number's divisibility and relationships with other numbers.
-
Place Value: Understanding place value is crucial for performing calculations efficiently. In 240, the 2 represents 2 hundreds, the 4 represents 4 tens, and the 0 represents 0 ones.
-
Distributive Property: While not directly applicable to this specific problem, the distributive property (a x (b + c) = (a x b) + (a x c)) is a powerful tool for simplifying multiplication problems involving addition or subtraction.
-
Real-world Applications: Multiplication is fundamental to many real-world applications, from calculating areas and volumes to determining costs and proportions. Understanding the concepts behind simple problems like 6 x 2 x 20 lays the foundation for tackling more complex mathematical challenges.
Problem-Solving Strategies: Beyond the Numbers
Solving 6 x 2 x 20 effectively highlights several crucial problem-solving strategies:
-
Understanding the problem: Before jumping into calculations, take a moment to comprehend the question. What operation is required? What are the given numbers?
-
Choosing the right strategy: Different methods can lead to the same solution. Select the approach that feels most intuitive and efficient for you.
-
Breaking down complex problems: Large problems can be simplified by breaking them into smaller, manageable parts. This is especially useful in more advanced mathematical contexts.
-
Checking your work: After completing the calculation, take a moment to review your steps to ensure accuracy.
Frequently Asked Questions (FAQ)
Q: Is there only one correct way to solve 6 x 2 x 20?
A: No, there are multiple ways to solve this problem, as demonstrated in the different methods outlined above. The commutative and associative properties of multiplication allow for flexibility in the approach.
Q: What if the problem was 6 + 2 x 20?
A: This highlights the importance of the order of operations. According to PEMDAS/BODMAS, multiplication comes before addition. Therefore, the calculation would be: 2 x 20 = 40, then 6 + 40 = 46.
Q: How can I improve my multiplication skills?
A: Practice is key! Memorize multiplication tables, use flashcards, work through practice problems, and explore different calculation methods. The more you practice, the faster and more efficient you’ll become.
Q: What are some real-world examples where this type of calculation is used?
A: Calculating the total cost of 20 items costing $6 each and coming in packs of 2 would involve this calculation. Similarly, determining the volume of a rectangular prism with dimensions 6, 2, and 20 units would use this calculation.
Conclusion: The Significance of a Simple Problem
While seemingly trivial, the problem "6 x 2 x 20" provides a springboard for exploring fundamental mathematical concepts, problem-solving strategies, and efficient calculation methods. Understanding the underlying principles – the commutative and associative properties, order of operations, and the various techniques for simplifying calculations – empowers you to tackle more complex mathematical challenges with confidence and efficiency. The journey from a simple calculation to a deeper understanding of mathematical principles underscores the importance of building a solid foundation in arithmetic. This foundation serves as the bedrock for success in more advanced mathematical fields and real-world applications. The seemingly simple equation opens doors to a world of mathematical exploration and problem-solving skills.
Latest Posts
Latest Posts
-
Class 7 Rs Aggarwal Solution
Sep 17, 2025
-
Electron Configuration Of Magnesium 2
Sep 17, 2025
-
How To Neutralise Acidic Soil
Sep 17, 2025
-
Clothing In The Stone Age
Sep 17, 2025
-
What Is 80 Of 30
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 6x 2 X 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.