6.4 As A Mixed Number
thesills
Sep 15, 2025 · 5 min read
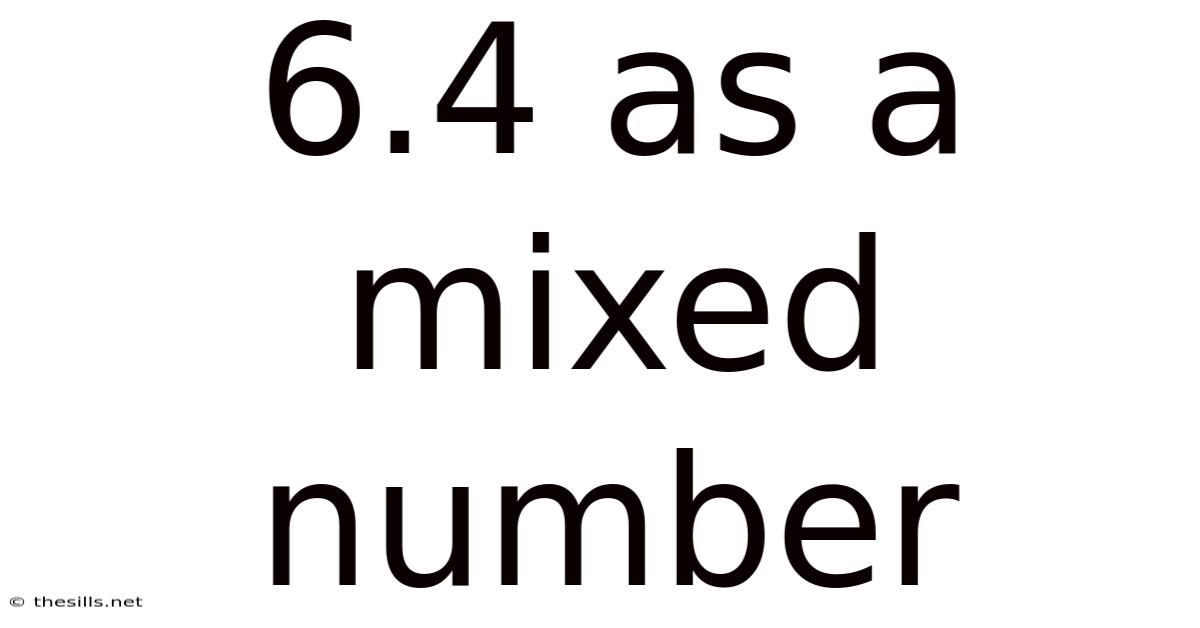
Table of Contents
Understanding 6.4 as a Mixed Number: A Comprehensive Guide
Representing decimal numbers as fractions, particularly as mixed numbers, is a fundamental skill in mathematics. This article delves into the process of converting the decimal number 6.4 into a mixed number, explaining the steps involved in a clear and concise manner, suitable for learners of all levels. We'll explore the underlying concepts, provide step-by-step instructions, and address frequently asked questions to ensure a thorough understanding of this important mathematical concept. This comprehensive guide will equip you with the knowledge and confidence to tackle similar conversions with ease.
Understanding Decimals and Mixed Numbers
Before diving into the conversion process, let's establish a clear understanding of the terms involved. A decimal number is a number that uses a decimal point to separate the whole number part from the fractional part. For example, in 6.4, '6' is the whole number part, and '.4' represents the fractional part.
A mixed number combines a whole number and a proper fraction (a fraction where the numerator is smaller than the denominator). For instance, 2 ¾ is a mixed number, where '2' is the whole number and '¾' is the proper fraction. Understanding the relationship between decimals and fractions is key to performing this conversion.
Converting 6.4 to a Mixed Number: A Step-by-Step Guide
The conversion of 6.4 to a mixed number involves several steps. Here's a detailed breakdown:
Step 1: Identify the Whole Number Part
The whole number part of the decimal 6.4 is clearly 6. This will form the whole number component of our mixed number.
Step 2: Convert the Decimal Part to a Fraction
The decimal part of 6.4 is 0.4. To convert this decimal to a fraction, we write it as a fraction with a denominator of a power of 10. Since 0.4 has one digit after the decimal point, we use 10 as the denominator:
0.4 = 4/10
Step 3: Simplify the Fraction (If Possible)
The fraction 4/10 can be simplified by finding the greatest common divisor (GCD) of the numerator (4) and the denominator (10). The GCD of 4 and 10 is 2. We divide both the numerator and the denominator by the GCD:
4 ÷ 2 = 2 10 ÷ 2 = 5
This simplifies the fraction to 2/5.
Step 4: Combine the Whole Number and the Simplified Fraction
Finally, we combine the whole number from Step 1 (6) with the simplified fraction from Step 3 (2/5) to form the mixed number:
6 + 2/5 = 6 2/5
Therefore, 6.4 as a mixed number is 6 2/5.
The Mathematical Rationale Behind the Conversion
The process of converting a decimal to a mixed number relies on the fundamental understanding of place value and fraction representation. The decimal system is based on powers of 10. Each digit to the right of the decimal point represents a fraction with a denominator that is a power of 10.
In the case of 6.4, the '4' in the tenths place represents 4/10. This fraction is then simplified to its lowest terms, 2/5, through the division by the greatest common divisor. This simplification maintains the equivalence of the fraction while representing it in its most concise form. The whole number part remains unchanged throughout the conversion process, simply combining with the simplified fraction to produce the final mixed number.
Alternative Methods for Conversion
While the step-by-step method outlined above is the most common and straightforward approach, there are alternative methods you can employ to convert decimals to mixed numbers. One such method is using equivalent fractions. For example, you can initially represent 0.4 as 4/10 and then find an equivalent fraction by multiplying both the numerator and the denominator by the same number. However, this method is less efficient than directly simplifying the initial fraction.
Illustrative Examples: Extending the Understanding
Let's consider a few more examples to solidify your understanding of this conversion process:
Example 1: Converting 3.75 to a Mixed Number
- Whole number part: 3
- Decimal part: 0.75 = 75/100
- Simplify the fraction: 75/100 = (75÷25) / (100÷25) = 3/4
- Mixed number: 3 + 3/4 = 3 ¾
Example 2: Converting 12.2 to a Mixed Number
- Whole number part: 12
- Decimal part: 0.2 = 2/10
- Simplify the fraction: 2/10 = 1/5
- Mixed number: 12 + 1/5 = 12 1/5
Example 3: Converting 8.125 to a Mixed Number
- Whole number part: 8
- Decimal part: 0.125 = 125/1000
- Simplify the fraction: 125/1000 = (125÷125) / (1000÷125) = 1/8
- Mixed number: 8 + 1/8 = 8 ⅛
Frequently Asked Questions (FAQ)
Q: What if the decimal has more than one digit after the decimal point?
A: The process remains the same. You write the digits after the decimal point as the numerator, and the denominator will be a power of 10 based on the number of digits. For instance, 0.123 would be 123/1000. Then, simplify the fraction to its lowest terms.
Q: Can all decimals be converted to mixed numbers?
A: Yes, but only terminating decimals (decimals that end) can be easily converted to fractions and then to mixed numbers. Recurring decimals (decimals that continue infinitely with repeating patterns) require a slightly different approach, often involving algebraic techniques.
Q: Why is simplifying the fraction important?
A: Simplifying the fraction gives you the most concise and accurate representation of the mixed number. It's a fundamental principle in mathematics to express fractions in their simplest form.
Q: What if the decimal part is 0?
A: If the decimal part is 0, then the number is already a whole number and is its own mixed number representation (e.g., 5.0 is the same as 5 0/1).
Conclusion
Converting decimals to mixed numbers is a crucial skill in mathematics. This process, while seemingly simple, underpins a deeper understanding of number systems, fractions, and the relationships between different numerical representations. By following the step-by-step guide and understanding the underlying mathematical principles, you can confidently convert any terminating decimal number into its equivalent mixed number form. Remember to always simplify the resulting fraction to its lowest terms to ensure a precise and concise representation. Through practice and application, this seemingly complex concept can be easily mastered.
Latest Posts
Latest Posts
-
Part Of A Doping Investigation
Sep 15, 2025
-
Darkest Part Of A Shadow
Sep 15, 2025
-
Include Units In Your Answer
Sep 15, 2025
-
25 4 As A Decimal
Sep 15, 2025
-
What Is Not A Macronutrient
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about 6.4 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.