5y 1 6x 4y 10
thesills
Sep 12, 2025 · 6 min read
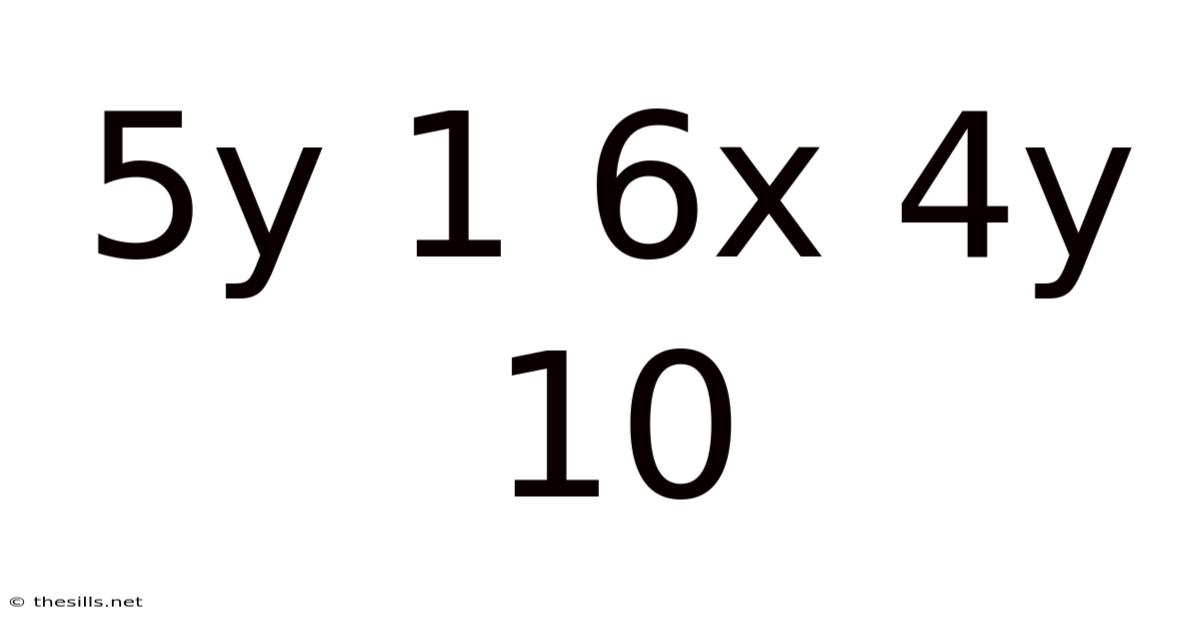
Table of Contents
Decoding the Mathematical Expression: 5y + 1 = 6x + 4y + 10
This article delves into the mathematical expression "5y + 1 = 6x + 4y + 10," exploring its solution, applications, and underlying concepts. Understanding this seemingly simple equation opens doors to more complex algebraic manipulations and problem-solving techniques. We'll break down the process step-by-step, making it accessible to learners of all levels, from beginners grappling with basic algebra to those seeking a refresher on fundamental principles.
Introduction: Understanding the Equation's Structure
The equation 5y + 1 = 6x + 4y + 10 is a linear equation in two variables, x and y. This means that when graphed, it represents a straight line. The goal is to find the values of x and y that satisfy the equation – meaning, when substituted into the equation, they make the left side equal to the right side. This contrasts with non-linear equations which, when graphed, produce curves rather than straight lines. Linear equations are fundamental to various fields, including physics, economics, and computer science, often representing relationships between two or more quantities.
Step-by-Step Solution: Isolating the Variables
Solving this equation involves manipulating it algebraically to isolate one variable in terms of the other. Let's begin by simplifying the equation:
-
Combine like terms: Notice that we have y terms on both sides of the equation. Subtracting 4y from both sides gives us:
5y - 4y + 1 = 6x + 4y - 4y + 10
This simplifies to:
y + 1 = 6x + 10
-
Isolate y: To isolate y, subtract 1 from both sides:
y + 1 - 1 = 6x + 10 - 1
This simplifies to:
y = 6x + 9
This equation is now in the slope-intercept form, y = mx + b, where m represents the slope (in this case, 6) and b represents the y-intercept (in this case, 9). This form is particularly useful for graphing the equation.
Graphical Representation and Interpretation
The equation y = 6x + 9 represents a straight line on a coordinate plane. The y-intercept is 9, meaning the line crosses the y-axis at the point (0, 9). The slope of 6 indicates that for every one-unit increase in x, y increases by six units. This positive slope means the line rises from left to right.
Key points to remember about the graph:
- The graph provides a visual representation of all possible solutions to the equation. Any point (x, y) that lies on the line satisfies the original equation.
- There are infinitely many solutions to this equation because there are infinitely many points on the line.
- To find specific solutions, you can substitute a value for either x or y into the equation and solve for the other variable. For example, if x = 1, then y = 6(1) + 9 = 15. So, (1, 15) is one solution.
Extending the Understanding: Systems of Equations
While we've solved for y in terms of x, a single linear equation with two variables doesn't have a unique solution. To find a unique solution, you need a system of equations, which involves two or more equations with the same variables. For example, consider the system:
- 5y + 1 = 6x + 4y + 10
- x + y = 5
We've already simplified the first equation to y = 6x + 9. We can now use this along with the second equation to solve for both x and y. There are several methods to solve systems of equations, including substitution and elimination. Using substitution:
-
Substitute: Substitute the expression for y from the first equation (y = 6x + 9) into the second equation (x + y = 5):
x + (6x + 9) = 5
-
Solve for x: Combine like terms and solve for x:
7x + 9 = 5 7x = -4 x = -4/7
-
Substitute and solve for y: Substitute the value of x back into either equation to solve for y. Using y = 6x + 9:
y = 6(-4/7) + 9 y = -24/7 + 63/7 y = 39/7
Therefore, the unique solution to this system of equations is x = -4/7 and y = 39/7.
Applications in Real-World Scenarios
Linear equations like this are ubiquitous in real-world applications. Here are a few examples:
- Economics: Supply and demand curves are often represented by linear equations. The point of intersection represents the market equilibrium price and quantity.
- Physics: Equations describing motion, such as velocity and acceleration, often involve linear relationships.
- Computer Science: Linear equations are used extensively in computer graphics, image processing, and machine learning algorithms.
- Engineering: Linear equations are fundamental to many engineering disciplines, including civil, mechanical, and electrical engineering.
Further Exploration: Non-Linear Extensions
The principles discussed here are fundamental to more advanced mathematical concepts. While this specific equation is linear, many real-world problems require the use of non-linear equations, which can involve exponents, logarithms, or trigonometric functions. Understanding linear equations is a crucial stepping stone to tackling these more complex challenges.
Frequently Asked Questions (FAQ)
Q: What if I get a different solution when solving the equation?
A: Double-check your algebraic manipulations. Even a small mistake can lead to an incorrect solution. Carefully review each step, paying attention to signs and operations. Using a different method (e.g., substitution instead of elimination) can sometimes help identify errors.
Q: Can this equation be solved graphically without solving algebraically first?
A: Yes. You can graph both equations (5y + 1 = 6x + 4y + 10 and a second equation, if you want a unique solution). The point where the lines intersect represents the solution to the system.
Q: What if there is no solution to the system of equations?
A: If the lines are parallel (have the same slope but different y-intercepts), there is no solution. This indicates the equations are inconsistent.
Q: What if there are infinitely many solutions?
A: If the lines are identical (same slope and same y-intercept), then there are infinitely many solutions. This indicates the equations are dependent.
Q: How can I improve my understanding of solving linear equations?
A: Practice is key. Work through numerous examples, trying different approaches. Consult textbooks, online resources, and seek help from teachers or tutors if needed.
Conclusion: Mastering Linear Equations
The equation 5y + 1 = 6x + 4y + 10, while seemingly simple, serves as a powerful illustration of fundamental algebraic principles. Solving this equation, and understanding its graphical representation, lays the groundwork for tackling more intricate mathematical problems. By mastering these basic techniques, you'll build a strong foundation for success in various academic and professional fields. Remember that consistent practice and a methodical approach are essential to mastering the art of solving linear equations. Keep exploring, keep questioning, and keep learning!
Latest Posts
Latest Posts
-
Woven Fabric Similar To Silk
Sep 12, 2025
-
Why Was The Zollverein Formed
Sep 12, 2025
-
Edwin Arnold Light Of Asia
Sep 12, 2025
-
Numbers With Only 3 Factors
Sep 12, 2025
-
Rotational Constant Of Diatomic Molecules
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 5y 1 6x 4y 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.