4x 2 X 1 0
thesills
Sep 14, 2025 · 5 min read
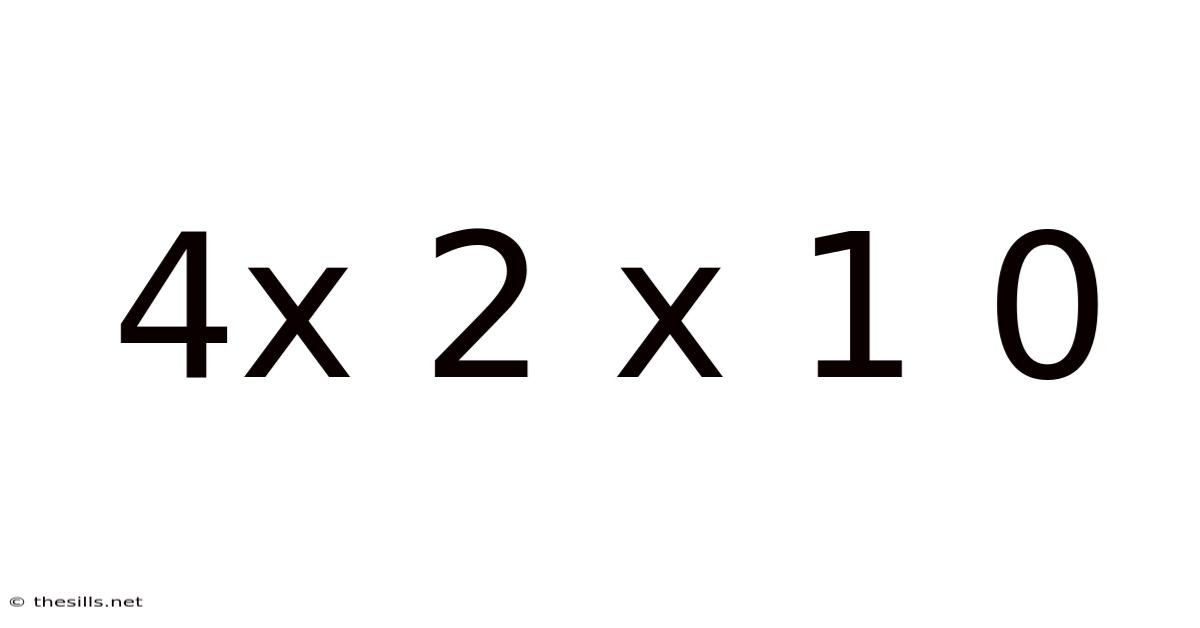
Table of Contents
Decoding the Mystery: A Deep Dive into 4 x 2 x 1 x 0
This seemingly simple mathematical expression, 4 x 2 x 1 x 0, hides a powerful concept that underpins much of arithmetic and algebra. While the answer is straightforward, understanding why the answer is what it is unlocks a deeper appreciation for the fundamental principles of multiplication and the properties of zero. This article will explore this expression, breaking down its calculation, explaining its underlying principles, and answering frequently asked questions. We'll delve into the significance of zero in mathematics and how it interacts with other numbers, making this seemingly simple equation a gateway to a richer understanding of mathematical operations.
Understanding the Problem: 4 x 2 x 1 x 0
At first glance, 4 x 2 x 1 x 0 appears to be a straightforward multiplication problem. We have four numbers: 4, 2, 1, and 0. The 'x' symbol indicates multiplication, meaning we need to multiply these numbers together in the order they are presented.
The beauty of mathematics lies in its consistent rules and predictable outcomes. The order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction), dictates the sequence in which we solve mathematical expressions. In this case, all operations are multiplication, so we can proceed from left to right.
Step-by-Step Calculation
Let's break down the calculation step by step:
-
4 x 2 = 8: We begin by multiplying 4 and 2. This is a basic multiplication fact.
-
8 x 1 = 8: Next, we multiply the result (8) by 1. Multiplying any number by 1 results in the same number. This is the multiplicative identity property.
-
8 x 0 = 0: Finally, we multiply the result (8) by 0. This is where the crucial understanding comes in. Any number multiplied by zero always equals zero. This is the zero property of multiplication.
Therefore, the answer to 4 x 2 x 1 x 0 is 0.
The Significance of Zero in Multiplication: The Zero Property
The zero property of multiplication is a fundamental concept in mathematics. It states that the product of any number and zero is always zero. This might seem intuitive, but it's a crucial rule that stems from the definition of multiplication itself.
Multiplication can be visualized as repeated addition. For example, 4 x 2 can be thought of as 4 + 4 = 8 (adding 4 two times). However, 4 x 0 means adding 4 zero times, resulting in a sum of zero. This concept extends to any number; multiplying any number by zero means we are not adding that number at all.
The zero property of multiplication is not just a rule; it is a consequence of the structure of the number system. It ensures that the operations of multiplication and addition are consistent and predictable. It plays a vital role in various mathematical concepts, including solving equations, working with polynomials, and understanding more advanced mathematical structures.
Beyond the Calculation: Exploring the Broader Implications
The simplicity of 4 x 2 x 1 x 0 belies its significance in illustrating several key mathematical concepts:
-
Order of Operations: The problem reinforces the importance of following the order of operations. While multiplication is commutative (the order doesn't matter for two numbers), the presence of zero highlights the importance of sequential calculations.
-
Multiplicative Identity: The multiplication by 1 demonstrates the multiplicative identity property. Multiplying any number by 1 leaves the number unchanged.
-
Distributive Property: While not directly used in this calculation, the zero property of multiplication is intricately connected to the distributive property (a(b + c) = ab + ac). Consider an expression like 5 x (2 + 0). The distributive property dictates that this equals (5 x 2) + (5 x 0) = 10 + 0 = 10. The zero property ensures that the second term disappears.
-
The Concept of Zero: The problem emphasizes the unique role of zero in the number system. Zero is neither positive nor negative; it's the additive identity (adding zero to a number doesn't change it) and, as shown here, it has a unique impact on multiplication.
Practical Applications
Understanding the zero property of multiplication isn't just an academic exercise. It has practical implications in various fields:
-
Programming: In computer programming, the zero property is crucial for controlling program flow and handling conditional statements.
-
Engineering: Engineers use this property in calculations involving forces, moments, and other quantities where zero values can represent the absence of a force or a particular condition.
-
Finance: In financial calculations, zero can represent the absence of an asset or a debt.
Frequently Asked Questions (FAQ)
Q: What happens if I change the order of the numbers?
A: While the order doesn't matter for most multiplication problems involving only non-zero numbers, the presence of zero changes the outcome if the order is altered. For instance, 0 x 4 x 2 x 1 still equals 0. However, the intermediate steps will be different.
Q: Can zero be divided by a number?
A: Yes, zero divided by any non-zero number equals zero (0/4 = 0). However, dividing a number by zero is undefined and leads to an error in mathematical calculations.
Q: What if there are multiple zeros in the multiplication?
A: The presence of multiple zeros will still result in a final answer of zero. For example, 4 x 2 x 1 x 0 x 0 x 0 = 0. The zero property of multiplication is absolute.
Q: Why is the zero property of multiplication so important?
A: The zero property ensures the consistency and predictability of the number system. It's essential for various mathematical operations, solving equations, and understanding more complex mathematical concepts. It simplifies calculations and allows for a consistent framework across various mathematical fields.
Conclusion: The Unassuming Power of 4 x 2 x 1 x 0
While seemingly straightforward, the expression 4 x 2 x 1 x 0 serves as a powerful reminder of fundamental mathematical concepts. The calculation itself is simple, but the underlying principles—the zero property of multiplication, the multiplicative identity, and the broader implications for the structure of the number system—are significant. Understanding these principles expands our mathematical literacy, providing a solid foundation for tackling more complex problems in arithmetic, algebra, and beyond. The seemingly simple equation is therefore a powerful gateway to a more comprehensive understanding of mathematics and its applications in various fields. It showcases that even the simplest mathematical expressions can hold profound mathematical significance.
Latest Posts
Latest Posts
-
Are Virtual Image Always Upright
Sep 14, 2025
-
Linear Mass Density Of String
Sep 14, 2025
-
Images Of Reflection Of Light
Sep 14, 2025
-
Where Is Market Gardening Practiced
Sep 14, 2025
-
Bones That Form The Elbow
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 4x 2 X 1 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.