4 X 5 X 1
thesills
Sep 13, 2025 · 6 min read
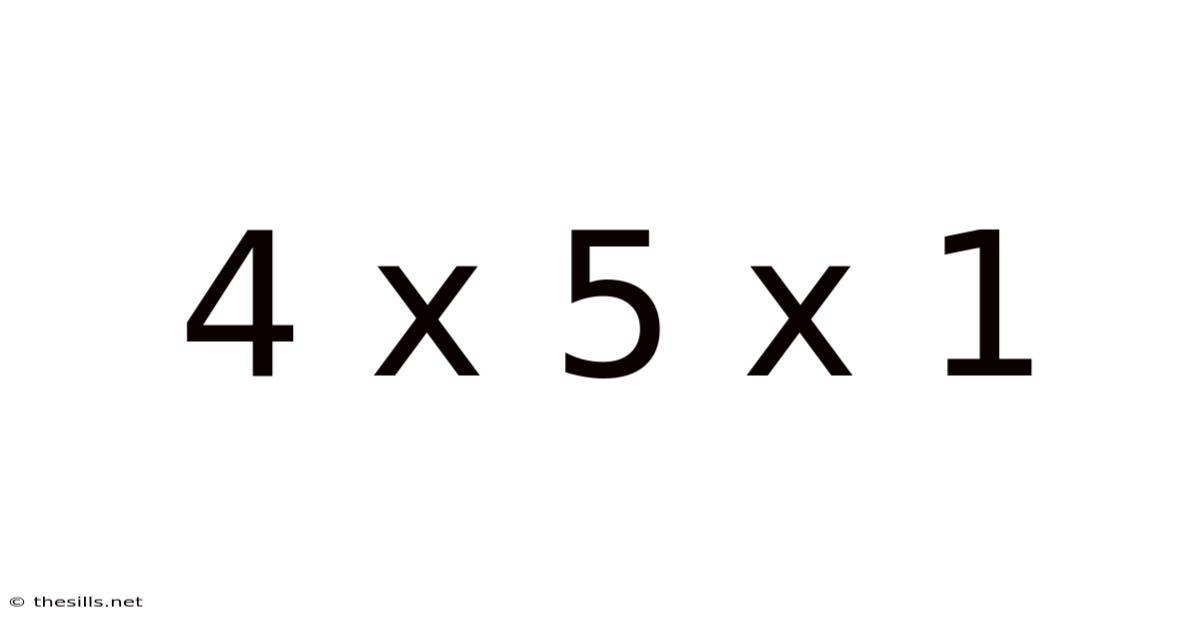
Table of Contents
Decoding 4 x 5 x 1: Exploring Dimensions, Volume, and Applications
This article delves into the seemingly simple expression "4 x 5 x 1," exploring its mathematical implications beyond basic multiplication, its representation in various contexts, and its surprising applications in diverse fields. We'll uncover how this seemingly straightforward calculation reveals fundamental concepts in geometry, physics, and even data analysis. Understanding this seemingly simple equation can unlock a deeper understanding of spatial reasoning and problem-solving.
Understanding the Basics: Multiplication and Dimensions
At its core, "4 x 5 x 1" represents a basic multiplication problem. The result, 20, is straightforward. However, the true significance lies in interpreting the three numbers as dimensions. We can visualize this as a rectangular prism (or cuboid) with:
- Length: 4 units
- Width: 5 units
- Height: 1 unit
This geometric interpretation opens up a world of possibilities beyond simple arithmetic.
Geometric Representation and Volume Calculation
The equation 4 x 5 x 1 directly relates to the calculation of the volume of the rectangular prism. Volume is the amount of three-dimensional space occupied by an object. In this case, the volume is calculated by multiplying the length, width, and height:
Volume = Length x Width x Height = 4 x 5 x 1 = 20 cubic units
This means the rectangular prism occupies 20 cubic units of space. The unit could be anything – centimeters, meters, inches, feet – depending on the context of the problem. The crucial point is that the number 20 represents a quantity of space.
Visualizing the Shape: From Abstract to Concrete
It's helpful to visualize this 4 x 5 x 1 rectangular prism. Imagine a rectangular box. Its base is a rectangle measuring 4 units by 5 units. The box's height is only 1 unit, making it a very flat box. This visualization helps solidify the concept of volume and dimensional representation. You could even build a physical model using blocks or draw it to scale on paper.
Extending the Concept: Different Units and Scalability
The units used are entirely arbitrary. The dimensions could be 4 meters x 5 meters x 1 meter, resulting in a volume of 20 cubic meters. Alternatively, it could be 4 centimeters x 5 centimeters x 1 centimeter, resulting in a volume of 20 cubic centimeters. The calculation remains the same; only the scale changes. This scalability is a crucial aspect of understanding dimensional analysis.
Applications Beyond Simple Geometry: Real-World Examples
The concept of calculating volume using three dimensions (like 4 x 5 x 1) is crucial in numerous real-world applications:
- Construction and Engineering: Calculating the volume of materials needed for construction projects, such as concrete for foundations or soil for landscaping.
- Packaging and Shipping: Determining the volume of a package to calculate shipping costs or optimize space utilization in warehouses.
- Manufacturing: Designing products and calculating the amount of raw materials required for production.
- Medicine and Biology: Determining the volume of fluids or tissues in medical imaging or biological research.
- Data Analysis: Representing and visualizing data in three dimensions, creating 3D histograms or scatter plots.
Exploring Variations: Manipulating Dimensions
Let's consider how changing the dimensions affects the volume:
- 4 x 1 x 5: Even though the numbers remain the same, changing the order changes our visual representation. This now describes a different orientation of the same rectangular prism. The volume remains 20 cubic units.
- 5 x 4 x 1: Similar to the previous example, this simply represents a different orientation; the volume is unchanged.
- 2 x 10 x 1: Here we have a different rectangular prism with the same volume. This illustrates that different dimensions can yield the same volume.
- 1 x 1 x 20: This is another example of a rectangular prism with the same volume but a very different shape. This emphasizes that volume alone doesn't define the shape.
Advanced Concepts: Surface Area and Other Calculations
Beyond volume, the dimensions of the 4 x 5 x 1 prism allow us to calculate other geometric properties:
- Surface Area: The total area of all the faces of the prism. This requires calculating the area of each face and summing them. The formula is more complex than volume calculation.
- Diagonal: The length of the diagonal line connecting opposite corners of the prism. This requires using the Pythagorean theorem in three dimensions.
Data Representation: 4 x 5 x 1 in Data Analysis
While seemingly simple, the concept of 4 x 5 x 1 can be applied to data representation. Imagine a data matrix:
- 4 rows: Representing four different data points or categories.
- 5 columns: Representing five different variables or features for each data point.
- 1 layer (depth): In this simple case, we only have a single layer of data. However, this can be extended to multiple layers to represent a three-dimensional dataset.
This 4 x 5 x 1 matrix could represent various datasets such as:
- Student performance: 4 students, 5 test scores.
- Sales data: 4 products, 5 regions, sales figures for one month.
Extending to Higher Dimensions
The concept of dimensions can extend beyond three. While we can easily visualize three dimensions, higher dimensions are used in advanced mathematics and physics. For instance, a 4 x 5 x 1 x 2 structure would represent a four-dimensional hyperrectangle, though visualization becomes more challenging.
Frequently Asked Questions (FAQ)
Q: Can the numbers in 4 x 5 x 1 be fractions or decimals?
A: Absolutely! The dimensions could be 4.5 x 5.2 x 1.1, for example. The calculation of the volume would simply involve multiplying the decimal numbers.
Q: What if one of the dimensions is zero?
A: If any of the dimensions is zero, the volume becomes zero. This represents a flat plane or a line, not a three-dimensional object.
Q: Are there any real-world limitations to applying the 4 x 5 x 1 model?
A: The limitations primarily come from real-world constraints. For example, manufacturing processes might not allow for perfectly precise dimensions, and materials might have irregularities affecting volume calculations.
Conclusion: The Power of Simple Geometry
The seemingly simple expression "4 x 5 x 1" unveils profound concepts related to geometry, volume calculation, data representation, and spatial reasoning. Understanding this basic equation provides a foundational understanding of dimensional analysis and its far-reaching applications in diverse fields. Its simplicity belies its power to help us understand and model the world around us, from the size of a box to complex datasets and advanced mathematical concepts. By appreciating the relationship between numbers and shapes, we unlock a deeper understanding of our physical and digital realities. This seemingly simple equation serves as a gateway to more advanced mathematical and scientific concepts, demonstrating the power of fundamental principles in shaping our understanding of the world.
Latest Posts
Latest Posts
-
Fructose Is An Example Of
Sep 13, 2025
-
X 4 2x 2 1
Sep 13, 2025
-
Is Co2 A Covalent Compound
Sep 13, 2025
-
When Bonds Form Energy Is
Sep 13, 2025
-
Integral Of 1 X 3
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 4 X 5 X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.