3x 2 2x 5 Factored
thesills
Sep 13, 2025 · 5 min read
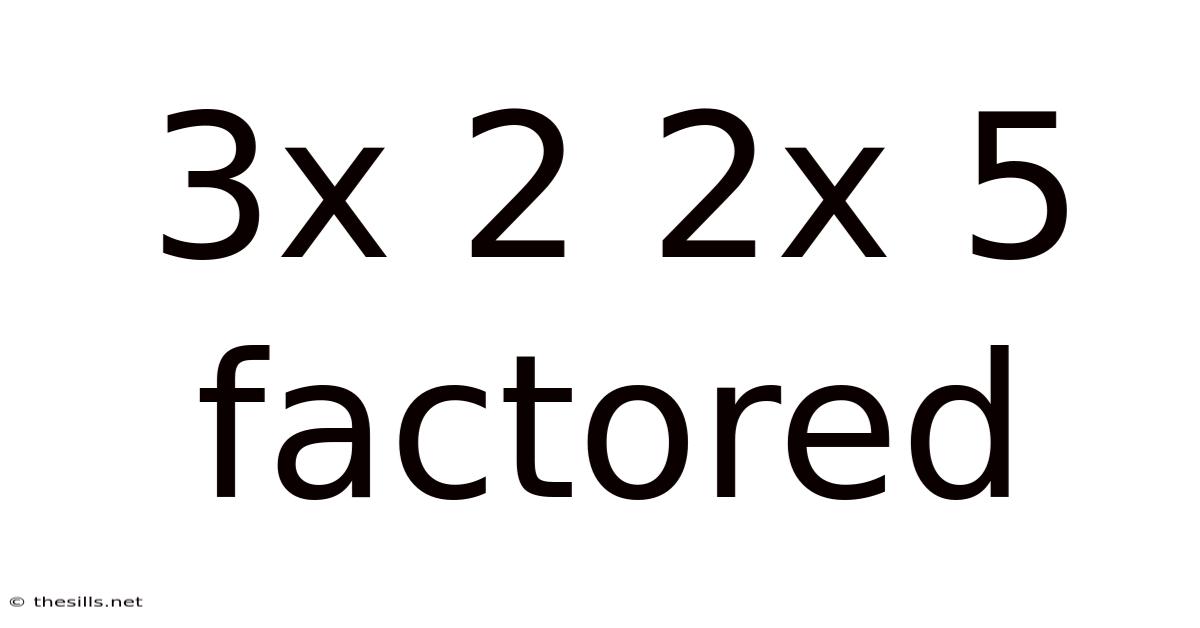
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into 3x² + 2x + 5
Factoring quadratic expressions is a fundamental skill in algebra. It's the process of rewriting a quadratic expression (an expression of the form ax² + bx + c, where a, b, and c are constants) as a product of simpler expressions. This article will explore the process of factoring, focusing specifically on the expression 3x² + 2x + 5 and providing a comprehensive understanding of the underlying principles and techniques involved. We'll delve into various methods, explaining when each is most effective and why this specific quadratic might present a unique challenge.
Introduction: Understanding Quadratic Expressions
Before we tackle 3x² + 2x + 5, let's review the basics. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. The general form is ax² + bx + c, where 'a', 'b', and 'c' are constants, and 'a' is not equal to zero. Factoring a quadratic expression involves finding two binomials (expressions with two terms) whose product is equal to the original quadratic. This process is crucial for solving quadratic equations, simplifying expressions, and understanding the behavior of parabolas (the graphical representation of quadratic functions).
Attempting to Factor 3x² + 2x + 5: The Challenges
The expression 3x² + 2x + 5 presents a specific challenge because it's not easily factorable using simple methods. Let's explore why:
- No Common Factor: There is no common factor (a number or variable that divides all terms) that can be factored out initially.
- Trial and Error: The traditional method of trial and error, where we try different combinations of factors of 'a' and 'c' to find the binomials, proves difficult here. Finding two numbers that add up to 'b' (2) and multiply to 'ac' (3 * 5 = 15) is not straightforward. No such integer combination exists.
Methods of Factoring Quadratic Expressions
Let's review the common methods used for factoring quadratics and why they might fail (or succeed) in this particular case:
-
Greatest Common Factor (GCF): This is the first step in any factoring problem. We look for a common factor among all terms. In our case, 3x² + 2x + 5 has no common factor other than 1.
-
Trial and Error: This method involves finding two binomials whose product equals the quadratic. We look for factors of 'a' and 'c' that add up to 'b'. For 3x² + 2x + 5, we'd need factors of 3 and 5 that add up to 2. This is not possible with integers.
-
AC Method (or Grouping): This method is particularly helpful when dealing with quadratics where trial and error proves cumbersome. The steps are:
- Find the product ac (3 * 5 = 15).
- Find two numbers that add up to b (2) and multiply to ac (15). In this case, no such integers exist.
- Rewrite the middle term (2x) as the sum of these two numbers and their corresponding x terms.
- Factor by grouping. Since we cannot find the required numbers, this method doesn't work.
-
Quadratic Formula: When other methods fail, the quadratic formula provides a definitive solution for finding the roots (or zeros) of the quadratic equation ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression 3x² + 2x + 5 = 0, we have:
x = [-2 ± √(2² - 4 * 3 * 5)] / (2 * 3) x = [-2 ± √(-56)] / 6
Notice that we have a negative number under the square root. This indicates that the roots are complex numbers (involving the imaginary unit 'i', where i² = -1). This confirms that the quadratic expression 3x² + 2x + 5 cannot be factored using real numbers.
Understanding Complex Numbers and Irreducible Quadratics
The appearance of a negative number under the square root in the quadratic formula signifies that the quadratic equation has no real roots. The solutions are complex conjugates – pairs of complex numbers of the form a + bi and a – bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit.
A quadratic expression that cannot be factored into real linear factors is called an irreducible quadratic over the real numbers. 3x² + 2x + 5 is an example of such an expression. It cannot be expressed as a product of two binomials with real coefficients.
Working with Complex Numbers
While 3x² + 2x + 5 cannot be factored over the real numbers, it can be factored over the complex numbers. Using the quadratic formula, we found the roots:
x = [-2 ± √(-56)] / 6 = [-2 ± 2i√14] / 6 = [-1 ± i√14] / 3
These are the roots of the quadratic equation. We can then express the quadratic as:
3x² + 2x + 5 = 3(x - ([-1 + i√14]/3))(x - ([-1 - i√14]/3))
This factorization utilizes complex numbers. It demonstrates that even though the expression is irreducible over the real numbers, it still possesses a factorization within the broader context of complex numbers.
Applications and Significance
Although the inability to factor 3x² + 2x + 5 using real numbers might seem like a limitation, it's important to understand that this scenario highlights the richness and depth of mathematics. The exploration of complex numbers is essential in various fields:
- Electrical Engineering: Complex numbers are fundamental in analyzing alternating current (AC) circuits.
- Quantum Mechanics: Complex numbers are inherent in the mathematical formulation of quantum theory.
- Signal Processing: Complex numbers play a vital role in analyzing and manipulating signals.
Conclusion: Embracing the Irreducible
The fact that 3x² + 2x + 5 is irreducible over the real numbers doesn't diminish its importance. It demonstrates the limitations of certain factoring methods and introduces the vital concept of complex numbers. Understanding this case helps solidify the understanding of quadratic equations and their solutions, expanding our mathematical knowledge beyond the realm of real numbers and preparing us for more advanced mathematical concepts. Remember, not all quadratic expressions can be easily factored using simple methods, and this is a valuable lesson in itself. The exploration of such problems enhances problem-solving skills and the ability to interpret mathematical results within different number systems. The quadratic formula provides a reliable method to find the roots, regardless of whether the expression is factorable using real numbers.
Latest Posts
Latest Posts
-
1cm To 1 Unit Graph
Sep 13, 2025
-
Steric Strain Vs Torsional Strain
Sep 13, 2025
-
Shorter Diagonal Of A Rhombus
Sep 13, 2025
-
Synonym For The Word Fallible
Sep 13, 2025
-
Allen Biology Race Answer Key
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 2x 5 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.