3x 2 11x 4 0
thesills
Sep 17, 2025 · 5 min read
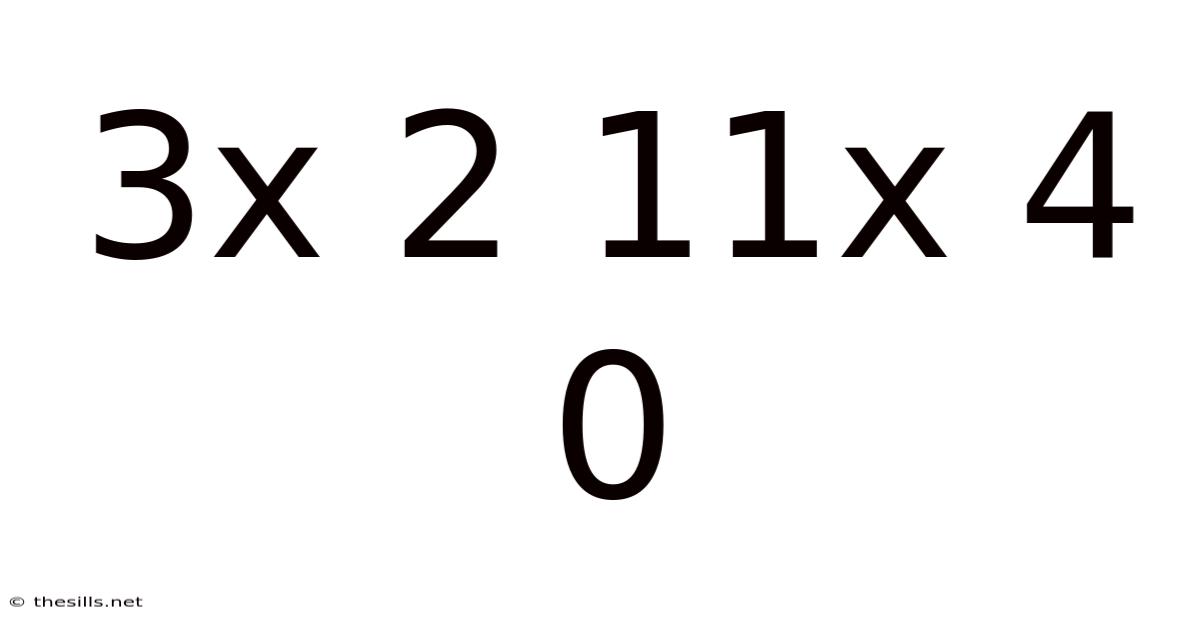
Table of Contents
Decoding the Enigma: Unraveling the Pattern in "3x 2 11x 4 0"
This article delves into the seemingly cryptic sequence "3x 2 11x 4 0," exploring potential patterns, mathematical relationships, and underlying logic. We'll investigate various approaches to decipher this sequence, considering possibilities from simple arithmetic progressions to more complex mathematical functions. The aim is not just to find a solution, but to illustrate the problem-solving process and demonstrate how different perspectives can lead to diverse interpretations. This exploration will be particularly useful for those interested in pattern recognition, mathematical reasoning, and code-breaking techniques.
Understanding the Puzzle: Initial Observations
The sequence "3x 2 11x 4 0" immediately presents a challenge. The inclusion of the multiplication symbol "x" disrupts a straightforward numerical progression. We can initially break down the sequence into three distinct parts: "3x 2," "11x 4," and "0." This segmentation suggests a possible pattern involving multiplication and potentially an underlying mathematical operation connecting these components.
However, the lack of explicit context makes it difficult to definitively determine a single "correct" answer. The solution likely hinges on identifying the rule or algorithm that governs the relationship between these numerical groups. The ambiguity introduces an element of creativity and encourages exploration of multiple possibilities.
Approach 1: Exploring Arithmetic Progressions and Variations
One immediate approach is to investigate if the numbers themselves form an arithmetic progression or a variation thereof. Let's examine the numbers independently of the "x" symbols: 3, 2, 11, 4, 0. At first glance, this does not exhibit a clear arithmetic sequence. However, we could explore transformations. For example:
-
Differences: Calculating the differences between consecutive numbers yields: -1, 9, -7, -4. This sequence doesn't reveal an obvious pattern.
-
Squares and Roots: Examining the square roots or squares of the numbers also doesn't immediately reveal a consistent pattern.
-
Modular Arithmetic: Investigating the remainders when dividing by a specific number (e.g., modulo 3, modulo 5) could potentially unveil hidden relationships, but this requires a systematic exploration of various moduli.
This approach demonstrates the need for flexibility. The initial lack of an evident arithmetic progression doesn't exclude the possibility that a hidden arithmetic pattern emerges after applying a suitable transformation or interpreting the sequence within a specific mathematical context.
Approach 2: Focusing on the Multiplication Symbol "x"
The presence of "x" suggests that multiplication plays a central role. We can analyze the "3x 2," "11x 4" segments individually:
- 3 x 2 = 6
- 11 x 4 = 44
Now, let's examine these results: 6 and 44. Do they show a pattern? At first, no apparent mathematical relationship stands out. However, we can consider different perspectives:
-
Differences: The difference between 44 and 6 is 38.
-
Ratios: The ratio of 44 to 6 is approximately 7.33, which doesn't immediately suggest a clear pattern.
-
Prime Factorization: The prime factorization of 6 is 2 x 3, while the prime factorization of 44 is 2 x 2 x 11. This shows the presence of common factors but doesn't yet illuminate a defining pattern.
The final element, "0," could be a crucial piece of information. It could indicate a termination point, a reset, or a specific condition within the underlying rule. We must consider its potential significance within the context of the multiplication results.
Approach 3: Exploring Potential Mathematical Functions
Beyond simple arithmetic, more complex mathematical functions could underlie the sequence. Consider possibilities such as:
-
Polynomial Functions: Could a polynomial function generate the numbers? This would require fitting a polynomial of sufficient degree to the sequence. Finding a polynomial that accurately represents the sequence would strongly suggest a mathematical relationship. However, determining the correct polynomial requires sophisticated techniques and is not readily apparent.
-
Recurrence Relations: A recurrence relation defines each term in the sequence as a function of previous terms. Exploring different recurrence relations could reveal a hidden pattern. However, the limited data points in the sequence constrain the possibilities.
-
Sequences Generated by Algorithms: It is possible the sequence is generated by a specific algorithm, perhaps involving conditional statements or iterative processes. Determining such an algorithm would require a thorough examination of possible computational procedures.
Approach 4: Considering Context and External Factors
The lack of context is a significant challenge. Without knowing the origin of the sequence or the intended purpose, finding a definitive answer is difficult. The sequence could represent:
-
A Code: It could be a simplified code or cipher.
-
Coordinates: The numbers could represent coordinates in a two-dimensional or multi-dimensional space.
-
Data Points: They could be data points from an experiment or observation, requiring further analysis to determine the underlying process.
-
Part of a Larger Sequence: It could be a segment extracted from a longer, more comprehensive sequence.
This demonstrates how the meaning of "3x 2 11x 4 0" depends entirely on its context. Without additional information, we are left to speculate based on patterns and mathematical relationships within the limited data provided.
Frequently Asked Questions (FAQs)
Q: Is there only one correct answer to this puzzle?
A: No, without additional information or context, there's no single "correct" answer. Multiple interpretations and solutions are plausible depending on the assumptions made about the underlying rules or generating process.
Q: What are some common mistakes people make when trying to solve this type of puzzle?
A: Common mistakes include prematurely assuming a simple arithmetic pattern, neglecting to consider the "x" symbols, and not exploring alternative mathematical functions or contexts. Overlooking the possibility of transformations or the role of the "0" are also frequent errors.
Q: How can I improve my skills in solving similar pattern-recognition puzzles?
A: Practice is crucial. Work on diverse puzzles involving number sequences, geometric patterns, and logic problems. Develop a systematic approach involving observation, hypothesis formation, testing, and refinement. Familiarize yourself with various mathematical concepts and techniques.
Conclusion: The Importance of Context and Multiple Perspectives
The sequence "3x 2 11x 4 0" presents a fascinating challenge, highlighting the importance of context and the value of exploring multiple approaches. While a definitive solution remains elusive without additional information, the process of attempting to decode this sequence demonstrates the power of mathematical reasoning, pattern recognition, and creative problem-solving. The ambiguous nature of the puzzle encourages exploration and reinforces the notion that multiple solutions can be valid depending on the assumptions and perspectives applied. This exercise underlines the need for flexibility and systematic investigation when confronting seemingly cryptic numerical sequences or patterns. Further research into specific mathematical domains might yield more specific solutions but, for now, the multiplicity of interpretations allows for a rich and stimulating exploration of mathematical thinking.
Latest Posts
Latest Posts
-
3 X 2 2x 1
Sep 17, 2025
-
X 3 X 4 1
Sep 17, 2025
-
Does A Liquid Have Volume
Sep 17, 2025
-
51 100 As A Decimal
Sep 17, 2025
-
Lialh4 Reaction With Carboxylic Acid
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 3x 2 11x 4 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.