37 1/2 As A Decimal
thesills
Sep 13, 2025 · 5 min read
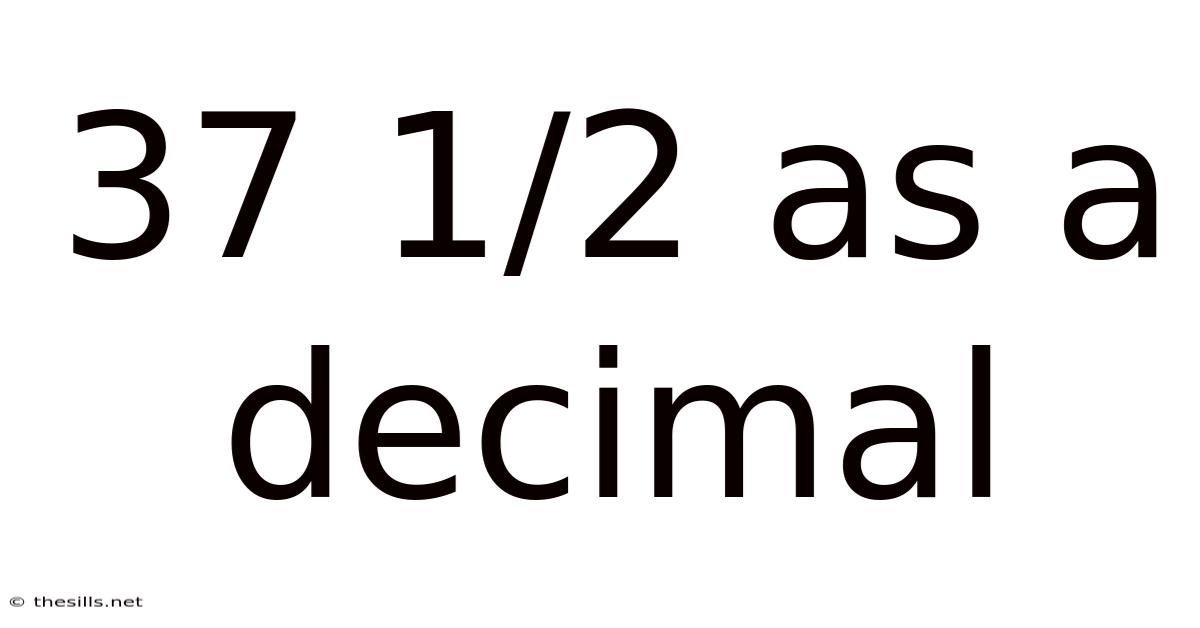
Table of Contents
37 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will explore the conversion of the mixed number 37 1/2 into its decimal equivalent, providing a step-by-step process, explanations of underlying principles, and addressing frequently asked questions. This will equip you with a thorough understanding of this simple yet crucial mathematical concept.
Introduction: Decimals and Fractions
Before diving into the conversion of 37 1/2, let's briefly review the relationship between decimals and fractions. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal is another way of representing a part of a whole, using a base-ten system. The decimal point separates the whole number part from the fractional part. Converting between fractions and decimals involves understanding this fundamental equivalence.
Step-by-Step Conversion of 37 1/2 to Decimal
There are several ways to convert the mixed number 37 1/2 into a decimal. Let's explore the most common and straightforward approaches:
Method 1: Converting the Fraction to a Decimal and Adding the Whole Number
This method involves first converting the fractional part (1/2) to a decimal and then adding it to the whole number part (37).
-
Convert the fraction to a decimal: The fraction 1/2 represents one divided by two. Performing this division gives us 0.5.
-
Add the whole number: Now, add the decimal equivalent of the fraction (0.5) to the whole number (37). This results in 37 + 0.5 = 37.5
Therefore, 37 1/2 as a decimal is 37.5.
Method 2: Converting the Mixed Number to an Improper Fraction, Then to a Decimal
This method involves first converting the mixed number into an improper fraction and then performing the division to obtain the decimal equivalent.
-
Convert to an improper fraction: To convert 37 1/2 to an improper fraction, we multiply the whole number (37) by the denominator (2) and add the numerator (1). This gives us (37 * 2) + 1 = 75. The denominator remains the same, so the improper fraction is 75/2.
-
Divide the numerator by the denominator: Now, divide the numerator (75) by the denominator (2). This yields 37.5.
Therefore, again, 37 1/2 as a decimal is 37.5.
Understanding the Underlying Principles
The conversion from fractions to decimals fundamentally relies on the concept of division. A fraction is essentially a division problem. The numerator is divided by the denominator. The result of this division is the decimal equivalent. In the case of 37 1/2, we are dividing 1 by 2, which gives us 0.5. This decimal is then added to the whole number portion, yielding 37.5.
The process of converting a mixed number to an improper fraction is a crucial step in many mathematical operations. It allows for simplification and easier manipulation of the fraction. Converting to an improper fraction facilitates the division process, resulting in a clean decimal equivalent.
Further Exploration: Different Fraction Types
While 37 1/2 is a straightforward example, let's consider how to handle other types of fractions:
-
Fractions with denominators that are powers of 10: Fractions like 1/10 (0.1), 3/100 (0.03), or 7/1000 (0.007) are easily converted to decimals because the denominators are powers of 10. The number of decimal places is determined by the number of zeros in the denominator.
-
Fractions with denominators that are not powers of 10: For fractions like 1/3 or 2/7, the conversion to decimal involves long division. These fractions produce recurring or repeating decimals (e.g., 1/3 = 0.3333...).
-
Complex fractions: These involve fractions within fractions. To convert these to decimals, simplify the complex fraction to a single fraction first and then perform the division.
Frequently Asked Questions (FAQs)
-
Why is understanding fraction-to-decimal conversion important? This skill is crucial in various fields, including science, engineering, finance, and everyday life. It's essential for accurately representing and manipulating quantities.
-
Are there any shortcuts for converting certain fractions to decimals? Yes, memorizing the decimal equivalents of common fractions like 1/2 (0.5), 1/4 (0.25), 1/5 (0.2), 1/8 (0.125), and 1/10 (0.1) can greatly speed up the conversion process.
-
What if the decimal conversion results in a repeating decimal? Repeating decimals are often represented by using a bar above the repeating digits (e.g., 0.333... is represented as 0.3̅). You can round the decimal to a certain number of decimal places depending on the required level of accuracy.
-
Can I use a calculator to convert fractions to decimals? Yes, most calculators have a fraction-to-decimal conversion function. Simply enter the fraction and press the appropriate key (often marked as "S⇔D" or a similar symbol) to obtain the decimal equivalent.
-
How can I improve my understanding of fractions and decimals? Practice is key. Solve numerous conversion problems, work through examples, and utilize online resources or educational materials to reinforce your understanding of these concepts.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting fractions to decimals is a fundamental skill that builds a strong foundation for further mathematical understanding. The conversion of 37 1/2 to 37.5, as demonstrated in this guide, illustrates the simple yet important procedures involved. By mastering these techniques and understanding the underlying principles, you can confidently handle more complex fraction-to-decimal conversions and apply this knowledge to a wide range of mathematical problems. Remember to practice regularly, and don't hesitate to explore additional resources to solidify your understanding. With consistent effort, you can become proficient in this essential mathematical skill.
Latest Posts
Latest Posts
-
Love Is Not Times Fool
Sep 13, 2025
-
What Happened To Max Power
Sep 13, 2025
-
Clock Hands Which Is Which
Sep 13, 2025
-
Chemical Formula In A Sentence
Sep 13, 2025
-
What Was The Question Again
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 37 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.