3 Is What Of 5
thesills
Sep 13, 2025 · 6 min read
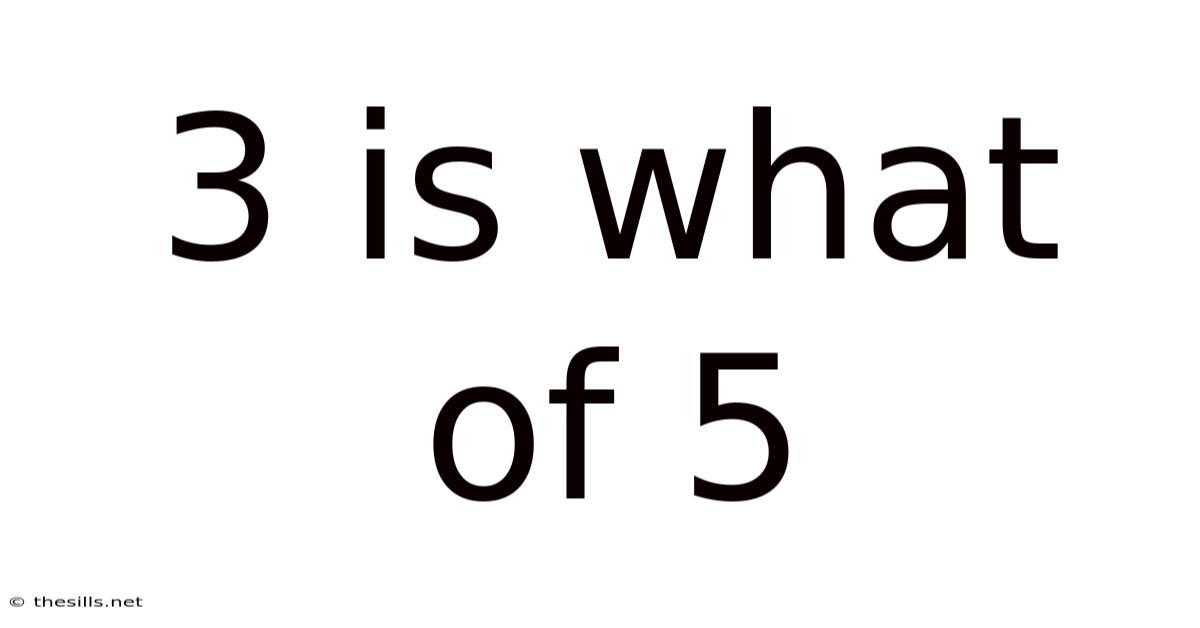
Table of Contents
Understanding Fractions: 3 is What Fraction of 5?
This article explores the fundamental concept of fractions, specifically addressing the question: "3 is what fraction of 5?" We'll delve into the meaning of fractions, how to represent them, and different methods for solving this type of problem. Understanding fractions is crucial for various aspects of mathematics and everyday life, from baking to budgeting, and this guide will provide a comprehensive understanding, suitable for learners of all levels. We'll cover the core concepts, provide step-by-step solutions, and address common questions about fractional representation.
Understanding Fractions: The Basics
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 1/2 (one-half), the numerator is 1 and the denominator is 2. This means you have one part out of two equal parts.
Fractions can represent various situations: a portion of a pizza, a segment of a journey, or a percentage of a total amount. Understanding fractions is key to grasping more advanced mathematical concepts such as decimals, percentages, ratios, and proportions.
Solving "3 is What Fraction of 5?"
The question "3 is what fraction of 5?" asks us to express the relationship between the number 3 (the part) and the number 5 (the whole) as a fraction. We can represent this problem directly as a fraction:
3/5
This fraction means 3 parts out of a total of 5 equal parts. The number 3 is the numerator (the part we're interested in), and the number 5 is the denominator (the total number of parts). This fraction is already in its simplest form because 3 and 5 share no common factors other than 1.
Different Approaches to Solving Fraction Problems
While the above method is the most direct way to answer "3 is what fraction of 5?", let's explore other approaches that can help solidify the understanding of fractions and their representation. These methods are particularly useful when dealing with more complex problems.
Method 1: Using the Definition of a Fraction
This method directly applies the definition of a fraction. We know that a fraction represents a part of a whole. In this case, the "part" is 3, and the "whole" is 5. Therefore, the fraction is simply 3/5.
Method 2: Visual Representation
Visual aids can be incredibly helpful, especially when first learning about fractions. Imagine you have 5 identical objects (e.g., apples, blocks, or circles). If you take 3 of these objects, the fraction representing the portion you have is 3/5. This visual representation reinforces the meaning of the numerator (the number of objects you have) and the denominator (the total number of objects).
Method 3: Solving for an Unknown Fraction
Sometimes, the problem might be presented slightly differently, requiring you to solve for an unknown fraction. For instance, a problem might state: "3 is x/5 of 5." In this case, you would solve for 'x'. The equation would look like this:
3 = (x/5) * 5
To solve for 'x', we simplify the equation:
3 = x
This confirms that 3 is 3/5 of 5.
Extending the Concept: Equivalent Fractions
It's important to understand the concept of equivalent fractions. These are fractions that represent the same value even though they look different. For example, 3/5, 6/10, and 9/15 are all equivalent fractions. They all represent the same proportion—three-fifths.
To find equivalent fractions, you multiply or divide both the numerator and the denominator by the same number (other than zero). For example:
- Multiplying both the numerator and denominator of 3/5 by 2 gives 6/10.
- Multiplying both by 3 gives 9/15.
Converting Fractions to Decimals and Percentages
Fractions, decimals, and percentages are all different ways of representing parts of a whole. You can easily convert between them.
To convert a fraction to a decimal, you simply divide the numerator by the denominator. For 3/5:
3 ÷ 5 = 0.6
To convert a fraction to a percentage, you multiply the decimal equivalent by 100 and add a percentage sign. For 0.6:
0.6 * 100 = 60%
Therefore, 3 is 60% of 5.
Real-World Applications of Fractions
The concept of fractions extends far beyond the classroom. Here are some examples of how fractions are used in everyday life:
- Cooking and Baking: Recipes often call for fractional amounts of ingredients (e.g., 1/2 cup of sugar, 2/3 cup of flour).
- Measurement: Measuring tools like rulers and tape measures often use fractions (e.g., 1/4 inch, 1/8 inch).
- Money: Dealing with cents represents a fraction of a dollar (e.g., 25 cents is 1/4 of a dollar).
- Time: Telling time involves fractions (e.g., half an hour, a quarter of an hour).
- Data Analysis: Data analysis frequently involves representing data as fractions or proportions.
Frequently Asked Questions (FAQ)
Q: Can a fraction have a denominator of 0?
A: No, a fraction cannot have a denominator of 0. Division by zero is undefined in mathematics.
Q: How do I simplify a fraction?
A: To simplify a fraction, find the greatest common divisor (GCD) of the numerator and denominator, and divide both by the GCD. For example, to simplify 6/10, the GCD of 6 and 10 is 2. Dividing both by 2 gives 3/5.
Q: What if I have a mixed number (a whole number and a fraction)?
A: To work with mixed numbers, you can convert them to improper fractions (where the numerator is larger than the denominator). For example, 1 1/2 is equivalent to 3/2.
Q: How do I add, subtract, multiply, and divide fractions?
A: There are specific rules for each operation. Adding and subtracting fractions require a common denominator, while multiplying involves multiplying the numerators and denominators separately. Dividing fractions involves inverting the second fraction and multiplying. These operations are best explained in more detailed guides on fraction arithmetic.
Conclusion: Mastering Fractions
Understanding fractions is a fundamental skill in mathematics and has wide-ranging applications in various aspects of life. The question "3 is what fraction of 5?" provides a simple yet important introduction to this crucial concept. By grasping the basic principles of fractions, their representation, and various methods for solving related problems, you build a solid foundation for tackling more complex mathematical challenges. Remember that practice is key to mastering this essential mathematical skill. Continue to explore different fraction problems and apply these concepts to real-world situations to build confidence and proficiency. The more you practice, the more intuitive fractions will become.
Latest Posts
Latest Posts
-
Over Irrigation Can Result In
Sep 13, 2025
-
What Is A Mixed Nerve
Sep 13, 2025
-
What Are Frog Hands Called
Sep 13, 2025
-
Sound Waves Are Mechanical Waves
Sep 13, 2025
-
Is Sodium Carbonate A Base
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 3 Is What Of 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.