2sin 2x Sinx 1 0
thesills
Sep 13, 2025 · 5 min read
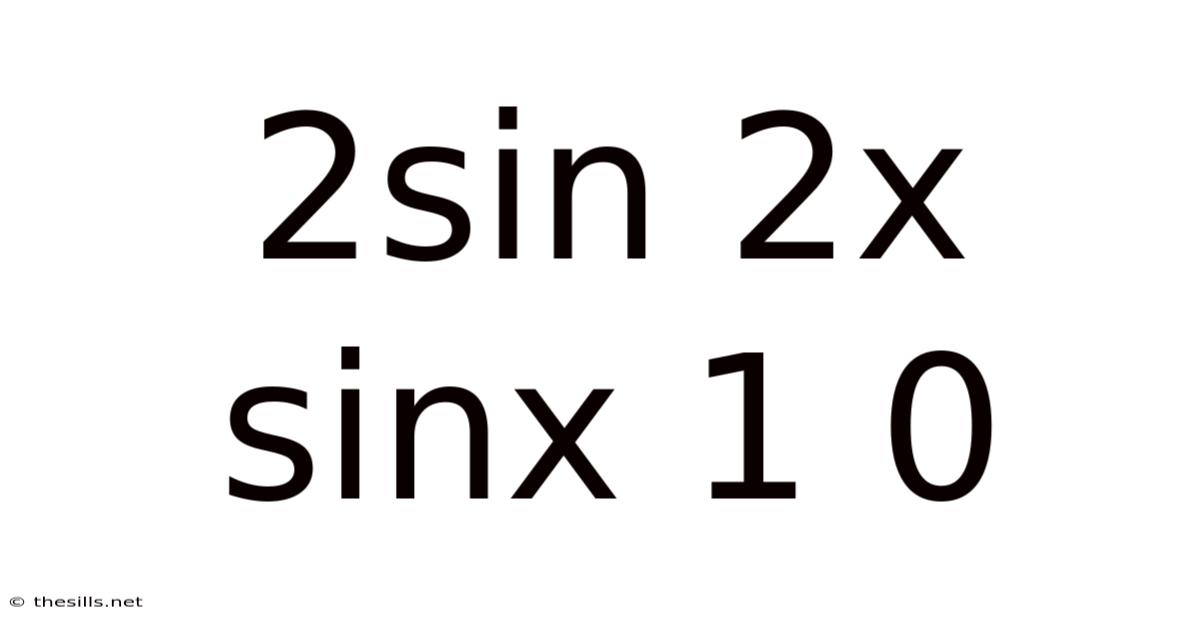
Table of Contents
Solving the Trigonometric Equation: 2sin(2x)sinx = 1
This article delves into the solution of the trigonometric equation 2sin(2x)sinx = 1. We will explore various methods to solve this equation, including employing trigonometric identities, understanding the unit circle, and analyzing the graphical representation. This comprehensive guide is designed for students and anyone interested in deepening their understanding of trigonometry. We will also address frequently asked questions and provide a detailed explanation of the underlying mathematical principles.
Introduction: Understanding the Equation
The equation 2sin(2x)sinx = 1 presents a challenge requiring a strong grasp of trigonometric identities and problem-solving strategies. Our goal is to find all possible values of 'x' that satisfy this equation. The key to solving this lies in strategically applying trigonometric identities to simplify the equation and isolate 'x'. We'll explore multiple approaches to reach the solution, ensuring a complete and comprehensive understanding. The equation involves the double-angle formula for sine, making it a rich example of how trigonometric identities can be used to solve complex equations.
Method 1: Using Trigonometric Identities
The most direct approach is to utilize the double-angle identity for sine: sin(2x) = 2sinxcosx. Substituting this into our original equation, we get:
2(2sinxcosx)sinx = 1
This simplifies to:
4sinx²cosx = 1
This equation now involves both sine and cosine, making direct solution challenging. We can, however, use the Pythagorean identity sin²x + cos²x = 1 to express cosx in terms of sinx: cosx = ±√(1 - sin²x). Substituting this yields:
4sinx²(±√(1 - sin²x)) = 1
This equation is rather complex and doesn't readily provide an analytical solution. Let's explore another method.
Method 2: Product-to-Sum Formula
Another powerful technique involves using the product-to-sum formulas. Recall the identity:
sinA sinB = (1/2)[cos(A-B) - cos(A+B)]
Applying this to our equation, with A = 2x and B = x, we get:
2 * (1/2)[cos(2x-x) - cos(2x+x)] = 1
Simplifying:
cos(x) - cos(3x) = 1
This equation is still complex but presents a more manageable path to a solution. We can use the triple-angle formula for cosine: cos(3x) = 4cos³x - 3cosx. Substituting this gives:
cosx - (4cos³x - 3cosx) = 1
Rearranging the terms, we have:
4cos³x - 4cosx + 1 = 0
This is a cubic equation in cosx. While solving cubic equations can be involved, numerical methods or specialized techniques can be employed to find the roots. Let's explore a graphical approach for a better understanding.
Method 3: Graphical Representation
Graphing the function y = 2sin(2x)sinx and the line y = 1 allows for a visual representation of the solutions. The points of intersection between the curve and the line represent the solutions to the equation. Using a graphing calculator or software, you can plot these functions and observe the points of intersection. This method is particularly helpful in visualizing the periodic nature of the solutions and estimating the values of x.
However, the graphical method alone doesn't provide precise analytical solutions. It primarily serves as a visualization tool and a means for approximating the solutions. The precision of the solution relies on the accuracy of the graphing tool.
Understanding the Solutions and their Periodicity
The original equation, 2sin(2x)sinx = 1, is a periodic function due to the trigonometric nature of sine. This means that solutions will repeat at regular intervals. The period of sinx is 2π, and the period of sin(2x) is π. The combined effect on the periodicity of the entire equation needs careful analysis. After obtaining potential solutions using any of the previously described methods (numerical solutions for the cubic equation in Method 2 or graphical interpretation in Method 3), you need to consider this periodicity to obtain a comprehensive set of solutions.
Numerical Methods for Solving the Cubic Equation
Method 2 resulted in a cubic equation: 4cos³x - 4cosx + 1 = 0. Solving cubic equations analytically can be cumbersome. Numerical methods, such as the Newton-Raphson method or the bisection method, provide efficient ways to approximate the roots of this equation. These methods involve iterative calculations, refining the approximation of the root with each iteration. This provides a numerical solution for cosx, which can then be used to find the corresponding values of x.
Remember that the solutions for cosx will likely be multiple, and each solution will lead to multiple solutions for x due to the periodicity of the cosine function.
Frequently Asked Questions (FAQ)
- Q: Can this equation be solved exactly without using numerical methods?
A: While a completely analytical solution avoiding all numerical approximation is challenging, a reduction to a cubic equation is possible, and in some specific cases, there might exist an analytical method. However, generally, numerical methods are necessary to obtain accurate and comprehensive solutions.
- Q: What is the significance of the double-angle formula in solving this equation?
A: The double-angle formula, sin(2x) = 2sinxcosx, is crucial because it allows us to express the equation in terms of only sinx and cosx, which then can be manipulated using other trigonometric identities.
- Q: How many solutions does this equation have?
A: Because of the periodic nature of the trigonometric functions involved, the equation has infinitely many solutions. However, within a given interval (e.g., 0 ≤ x < 2π), there will be a finite number of solutions.
- Q: How can I verify my solutions?
A: Once you have obtained potential solutions for x, substitute them back into the original equation, 2sin(2x)sinx = 1. If the equation holds true, then the solution is valid.
Conclusion: A Multifaceted Approach to Trigonometric Problem Solving
Solving the equation 2sin(2x)sinx = 1 requires a blend of theoretical understanding and practical application. We've explored three primary methods: utilizing trigonometric identities, employing the product-to-sum formula leading to a cubic equation, and using graphical representation. Each approach offers unique insights into the problem's structure and allows for different ways to approximate or obtain the solution set. Remember the importance of accounting for the periodicity of trigonometric functions when determining the complete set of solutions. This comprehensive analysis highlights the importance of mastering trigonometric identities and employing numerical methods when dealing with complex trigonometric equations. The understanding gained through solving this equation serves as a valuable foundation for tackling more intricate trigonometric problems in the future.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2sin 2x Sinx 1 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.