200 Percent In Decimal Form
thesills
Sep 17, 2025 · 6 min read
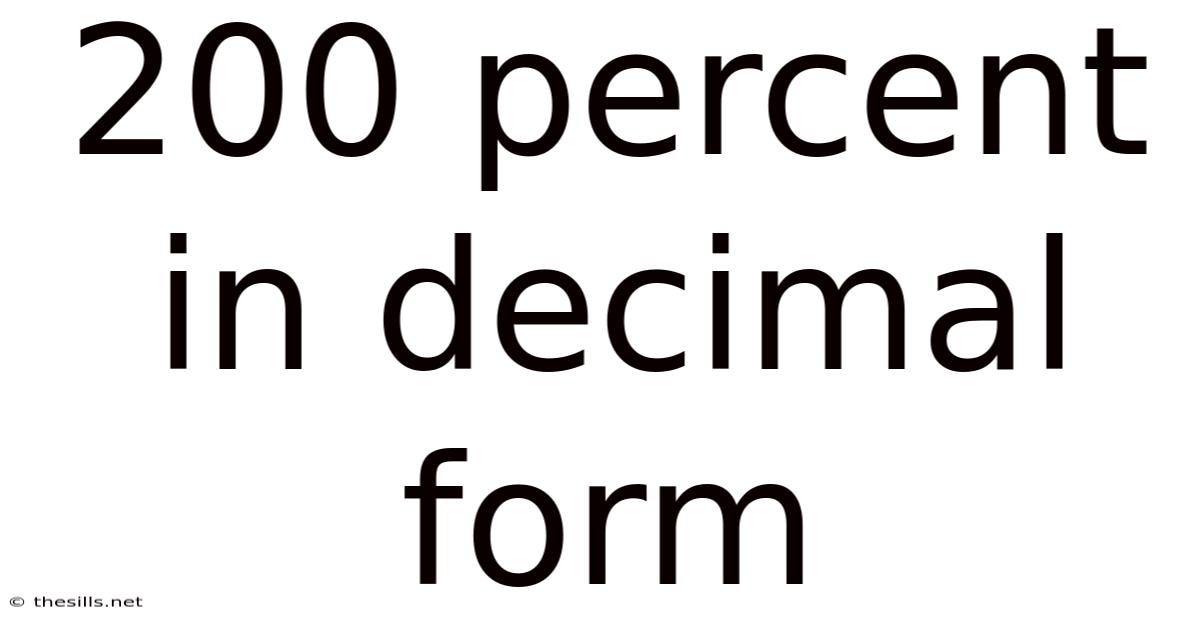
Table of Contents
Understanding 200 Percent: A Deep Dive into Decimal Conversions and Applications
What does 200 percent mean? It's more than just a simple number; it represents a crucial concept in mathematics and has widespread applications in various fields. This article will provide a comprehensive exploration of 200 percent, explaining its conversion to decimal form, its practical uses, and answering common questions about percentage calculations. We'll delve deep into the underlying principles, ensuring a solid understanding for readers of all levels.
Introduction: Percentages and Their Decimal Equivalents
Percentages are a way of expressing a fraction or ratio as a portion of 100. The word "percent" itself derives from the Latin "per centum," meaning "out of a hundred." Therefore, 100 percent (100%) represents the whole or the entirety of something. Any value above 100% indicates a quantity exceeding the original whole. Understanding how to convert percentages into decimal form is fundamental to many calculations. This is especially crucial when working with computers or calculators, which primarily utilize decimal notation. This article focuses specifically on understanding 200%, its decimal equivalent, and its broader implications.
Converting 200 Percent to Decimal Form: The Simple Method
Converting a percentage to a decimal is straightforward. The process involves dividing the percentage by 100. For 200 percent, the calculation is as follows:
200% ÷ 100 = 2.0
Therefore, 200 percent in decimal form is 2.0 or simply 2. This seemingly simple conversion holds significant implications, as we will explore further.
Understanding the Significance of 2.0: Beyond the Decimal
The decimal equivalent of 200% being 2 highlights a key concept: percentages greater than 100% represent quantities that are more than the original whole. If you have 100 apples, and you increase that by 200%, you now have 300 apples (100 + 200% of 100 = 100 + 200 = 300). The decimal 2 acts as a multiplier in this context, indicating a doubling of the original quantity.
This principle is vital in diverse applications, such as:
- Financial Calculations: Interest rates, profit margins, and investment returns are often expressed as percentages. A 200% return means your investment has doubled.
- Scientific Data Analysis: Percentage increases or decreases are frequently used to represent changes in experimental data. A 200% increase signifies a tripling of the original value.
- Business and Economics: Growth rates, market share changes, and inflation are often presented using percentages. A 200% increase in production signifies a tripling of output.
- Everyday Life: Sales discounts, price increases, and recipe scaling often involve percentage calculations. A 200% increase in a recipe ingredient would mean using three times the original amount.
Practical Applications: Real-world Examples of 200 Percent
Let's delve into some real-world examples to solidify our understanding of 200 percent:
Example 1: Investment Returns
Suppose you invested $1000 in a stock, and its value increased by 200%. To calculate the final value, we would perform the following calculation:
Increase = 200% of $1000 = 2.0 * $1000 = $2000 Final Value = Initial Value + Increase = $1000 + $2000 = $3000
Therefore, your investment is now worth $3000.
Example 2: Population Growth
Imagine a town with a population of 5000 people. If the population increases by 200% over a decade, we can calculate the new population:
Increase = 200% of 5000 = 2.0 * 5000 = 10000 New Population = Initial Population + Increase = 5000 + 10000 = 15000
The town's population would grow to 15,000.
Example 3: Price Increase
If the price of a product is $50, and it increases by 200%, the new price would be:
Increase = 200% of $50 = 2.0 * $50 = $100 New Price = Initial Price + Increase = $50 + $100 = $150
The price would become $150.
These examples illustrate the practical application of converting 200% to its decimal equivalent (2.0) for calculating increases. It's important to note that in each case, the original value is added to the increase to get the final result. This differs from scenarios involving percentage decreases, which require subtraction.
Beyond Simple Increases: More Complex Percentage Calculations
While our focus is on 200%, it's beneficial to understand how percentage calculations extend beyond simple increases. Consider these more complex scenarios:
- Percentage Decrease: If a value decreases by a certain percentage, you subtract the percentage of the original value from the original value. For example, a 50% decrease in 100 would be 100 - (0.5 * 100) = 50.
- Successive Percentage Changes: If a value undergoes multiple percentage changes, you must calculate each change sequentially. For example, a 100% increase followed by a 50% decrease doesn't result in the original value.
- Compound Interest: This involves calculating interest on both the principal amount and accumulated interest. Compound interest calculations require a more intricate formula involving exponents.
Understanding these nuances is crucial for accurate calculations in various contexts, especially finance and investment.
Frequently Asked Questions (FAQ)
Q1: What is the difference between 200% and 2?
A1: While 200% and 2 are numerically equivalent in terms of their value, they represent different ways of expressing the same quantity. 200% is a percentage, indicating a portion of 100, while 2 is a decimal or whole number, representing a direct numerical value. The context is crucial; using 200% helps in visualizing the proportional increase relative to the original quantity.
Q2: Can percentages be greater than 100%?
A2: Yes, absolutely. Percentages greater than 100% represent quantities exceeding the original whole. They are often used to show growth, increases, or values exceeding a baseline.
Q3: How do I convert a decimal to a percentage?
A3: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol. For example, 0.75 becomes 75%.
Q4: What are some common mistakes people make when working with percentages?
A4: Common errors include confusing percentage increases with percentage points, incorrectly calculating successive percentage changes, and failing to account for the original value when calculating percentage increases or decreases.
Q5: Where can I find more resources to learn about percentages?
A5: Many online resources, textbooks, and educational websites offer comprehensive explanations and practice exercises on percentage calculations.
Conclusion: Mastering Percentage Calculations
Understanding 200 percent and its decimal equivalent (2.0) is fundamental to various mathematical applications. Converting percentages to decimals is crucial for accurate calculations, particularly when using calculators or computers. This article has explored the simple conversion method, discussed practical applications in diverse fields, and addressed common questions. By mastering percentage calculations, you equip yourself with a powerful tool for understanding and analyzing data in numerous contexts. Remember that the key to success lies in understanding the underlying principles and practicing regularly. The ability to comfortably convert and utilize percentages, including values exceeding 100%, is a valuable skill that will benefit you in both academic and professional pursuits.
Latest Posts
Latest Posts
-
Factor X 2 10x 25
Sep 17, 2025
-
The Purchasing Cycle Begins With
Sep 17, 2025
-
What Is 4 579 Mm Solid
Sep 17, 2025
-
22 7 Is Rational Or Irrational
Sep 17, 2025
-
Root Mean Square Speed Units
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 200 Percent In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.