2 4 12 48 240
thesills
Sep 12, 2025 · 5 min read
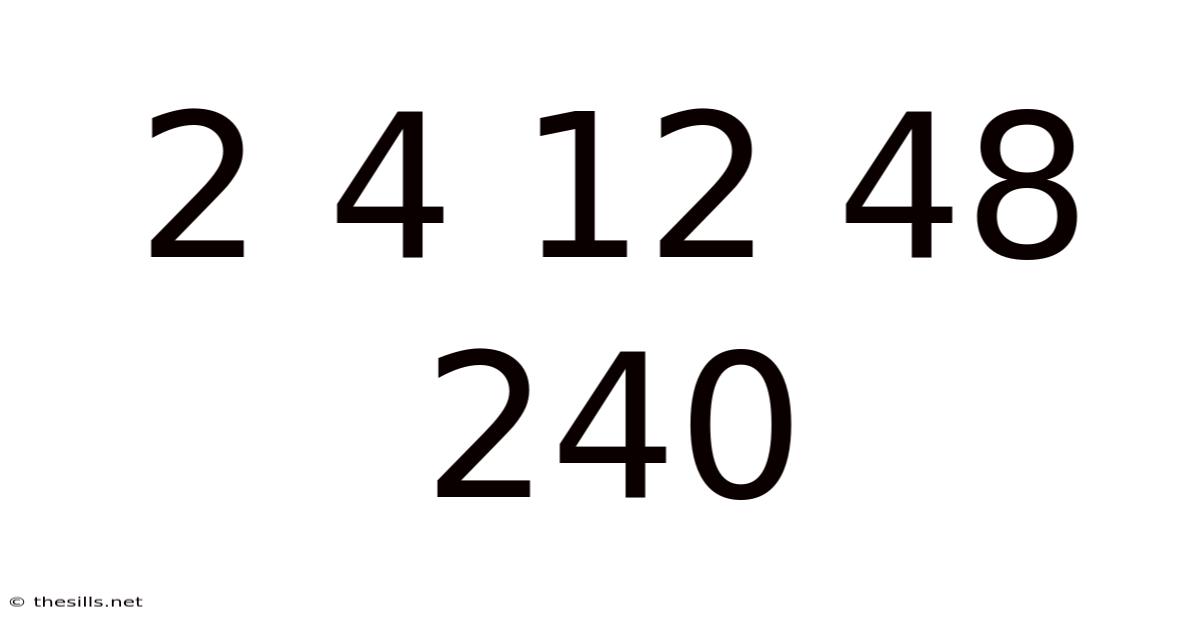
Table of Contents
Unraveling the Pattern: Exploring the Sequence 2, 4, 12, 48, 240
This article delves into the fascinating mathematical sequence: 2, 4, 12, 48, 240. We'll explore the pattern underlying these numbers, uncover the rule governing their progression, and examine different methods for predicting subsequent terms in the sequence. Understanding this sequence provides valuable insights into mathematical reasoning, pattern recognition, and the beauty of seemingly simple numerical relationships. We will also look at variations and extensions of this pattern to broaden your understanding of mathematical sequences.
Understanding the Pattern: A Visual Approach
At first glance, the sequence 2, 4, 12, 48, 240 might seem random. However, a closer inspection reveals a consistent pattern based on multiplication. Let's analyze the ratios between consecutive terms:
- 4 / 2 = 2
- 12 / 4 = 3
- 48 / 12 = 4
- 240 / 48 = 5
Notice a pattern? The ratio between each term and its preceding term increases by one. This suggests a recursive relationship where each term is obtained by multiplying the previous term by an increasing integer.
Defining the Recursive Rule
We can formally define the recursive rule for this sequence. Let's denote the nth term as a<sub>n</sub>. Then:
- a<sub>1</sub> = 2
- a<sub>n</sub> = a<sub>n-1</sub> * n (for n > 1)
This means:
- a<sub>2</sub> = a<sub>1</sub> * 2 = 2 * 2 = 4
- a<sub>3</sub> = a<sub>2</sub> * 3 = 4 * 3 = 12
- a<sub>4</sub> = a<sub>3</sub> * 4 = 12 * 4 = 48
- a<sub>5</sub> = a<sub>4</sub> * 5 = 48 * 5 = 240
This recursive rule clearly defines the sequence and allows us to generate any subsequent term.
Predicting Future Terms
Using the established recursive rule, we can easily predict future terms in the sequence:
- a<sub>6</sub> = a<sub>5</sub> * 6 = 240 * 6 = 1440
- a<sub>7</sub> = a<sub>6</sub> * 7 = 1440 * 7 = 10080
- a<sub>8</sub> = a<sub>7</sub> * 8 = 10080 * 8 = 80640
- and so on...
Beyond Recursion: An Explicit Formula
While the recursive rule is effective for generating subsequent terms, it doesn't provide a direct method for calculating a specific term without knowing the preceding ones. An explicit formula would be more efficient. Let's derive one.
Observe the pattern:
- a<sub>1</sub> = 2 = 2 * 1
- a<sub>2</sub> = 4 = 2 * 1 * 2
- a<sub>3</sub> = 12 = 2 * 1 * 2 * 3
- a<sub>4</sub> = 48 = 2 * 1 * 2 * 3 * 4
- a<sub>5</sub> = 240 = 2 * 1 * 2 * 3 * 4 * 5
This reveals that the nth term can be expressed as:
a<sub>n</sub> = 2 * n! (where n! denotes the factorial of n)
This explicit formula allows us to directly calculate any term in the sequence without needing to calculate all preceding terms. For example, to find a<sub>10</sub>, we simply compute 2 * 10! = 7,680,000.
Mathematical Connections and Extensions
This sequence isn't just a standalone curiosity. It connects to several important mathematical concepts:
-
Factorials: The sequence is intrinsically linked to the factorial function, a fundamental concept in combinatorics and probability.
-
Recursive Sequences: The sequence showcases the power and elegance of recursive definitions, which are widely used in various areas of mathematics and computer science.
-
Growth Patterns: The sequence demonstrates exponential growth, where the rate of increase accelerates with each term. This type of growth is observed in many real-world phenomena, such as population growth or compound interest.
Variations and Generalizations
We can generalize this sequence by changing the starting value. For instance, if we start with 3 instead of 2, the sequence becomes:
3, 6, 18, 72, 360...
The recursive rule remains similar: a<sub>n</sub> = a<sub>n-1</sub> * n, but the first term changes. The explicit formula would then be a<sub>n</sub> = 3 * n!.
We could also explore variations where the multiplier increases by a value other than 1. This opens up a whole family of related sequences with different properties.
Applications and Real-World Examples
While this specific sequence might not have direct, obvious real-world applications like some other mathematical concepts, the underlying principles are extremely relevant:
-
Modeling Growth: The exponential growth exhibited by the sequence can be used to model various real-world phenomena, from population growth to the spread of information in social networks, after suitable adjustments.
-
Algorithm Design: Recursive algorithms, inspired by the recursive definition of the sequence, are fundamental to computer science and are used in solving many problems efficiently.
Frequently Asked Questions (FAQ)
Q: Is this sequence unique?
A: No. Many other sequences could exhibit similar multiplicative growth patterns. This sequence is defined by its specific starting value (2) and the rule for incrementing the multiplier.
Q: Are there other ways to describe this sequence?
A: Yes, we could use different notations or focus on the differences between consecutive terms instead of the ratios.
Q: Can this sequence be represented graphically?
A: Absolutely. Plotting the terms against their index (1, 2, 3, 4, 5...) would reveal a rapidly increasing curve representing the exponential growth.
Q: What are some related mathematical concepts I could explore further?
A: You could explore more deeply into factorials, recursive relationships, series and sequences, generating functions, and exponential growth models.
Conclusion
The sequence 2, 4, 12, 48, 240, while seemingly simple, provides a rich opportunity to explore fundamental mathematical concepts such as recursion, factorials, and exponential growth. Understanding the recursive rule and deriving the explicit formula highlight the power of mathematical reasoning and pattern recognition. Moreover, the sequence serves as a gateway to further exploration of more advanced mathematical ideas, enriching our understanding of the intricate and beautiful world of numbers. The ability to analyze this seemingly simple sequence allows us to develop stronger analytical and problem-solving skills applicable to various fields, reinforcing the importance of fundamental mathematical concepts in broader contexts. The exponential growth represented in this sequence is also crucial in understanding numerous real-world phenomena, proving its practical significance beyond its initial simplicity. This exploration encourages further investigation into the fascinating world of mathematical patterns and their applications.
Latest Posts
Related Post
Thank you for visiting our website which covers about 2 4 12 48 240 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.