11/8 As A Mixed Number
thesills
Sep 17, 2025 · 5 min read
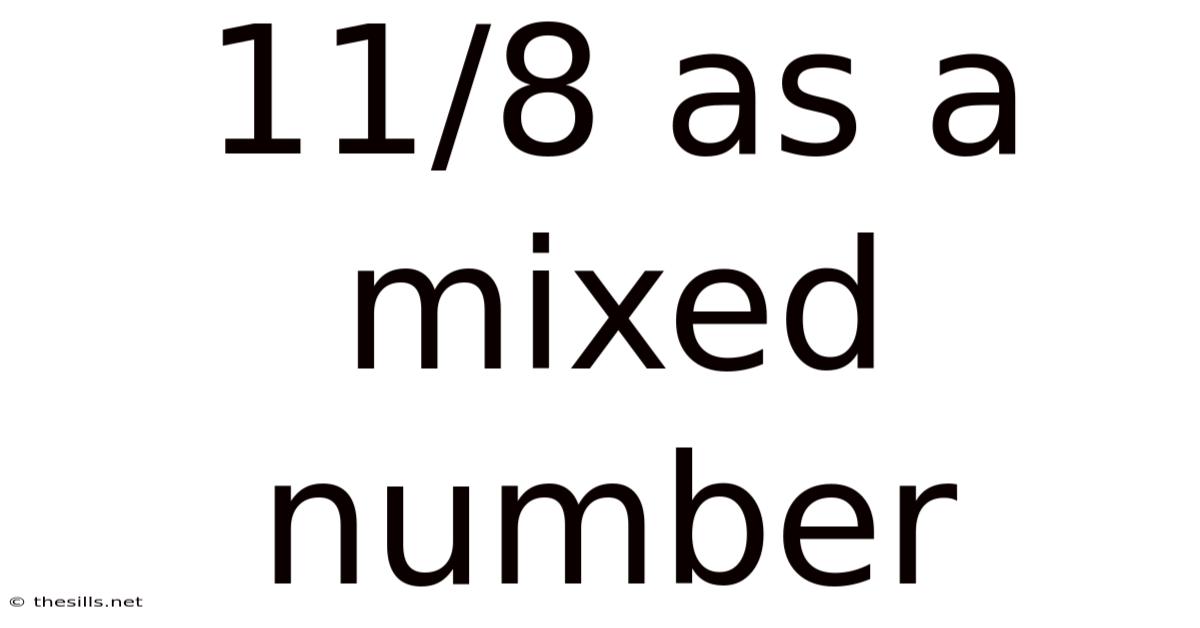
Table of Contents
Understanding 11/8 as a Mixed Number: A Comprehensive Guide
The fraction 11/8 represents a situation where the numerator (11) is larger than the denominator (8). This is known as an improper fraction. Understanding how to convert improper fractions, like 11/8, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will not only show you how to convert 11/8 into a mixed number but also delve into the underlying principles, provide practice examples, and address frequently asked questions. We'll explore the concept thoroughly, ensuring a solid grasp of this essential mathematical concept.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is one where the numerator is smaller than the denominator. For example, 1 ½, 3 ¼, and 2 ⅔ are all mixed numbers. They represent quantities that are greater than one whole unit but less than the next whole number. Understanding mixed numbers is crucial for various applications, from baking and cooking to construction and engineering.
Converting 11/8 to a Mixed Number: A Step-by-Step Approach
Converting an improper fraction to a mixed number involves dividing the numerator by the denominator. Let's break down the process for 11/8:
Step 1: Divide the numerator (11) by the denominator (8).
11 ÷ 8 = 1 with a remainder of 3.
Step 2: The quotient (1) becomes the whole number part of the mixed number.
This represents the number of whole times the denominator goes into the numerator.
Step 3: The remainder (3) becomes the numerator of the fractional part.
This represents the portion of the whole that is left over.
Step 4: The denominator remains the same (8).
The denominator represents the size of the parts.
Therefore, 11/8 as a mixed number is 1 ¾.
Visualizing the Conversion
Imagine you have 11 slices of pizza, and each pizza has 8 slices. You can make one whole pizza (8 slices) and have 3 slices remaining. This remaining 3 slices represents ¾ of a pizza. Hence, you have 1 whole pizza and ¾ of another, which is 1 ¾ pizzas. This visual representation helps solidify the concept of converting improper fractions to mixed numbers.
Further Examples: Converting Improper Fractions to Mixed Numbers
Let's practice with a few more examples to reinforce your understanding:
- 17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 ⅖.
- 23/6: 23 ÷ 6 = 3 with a remainder of 5. Therefore, 23/6 = 3 ⅚.
- 9/4: 9 ÷ 4 = 2 with a remainder of 1. Therefore, 9/4 = 2 ¼.
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand the reverse process: converting a mixed number back into an improper fraction. This involves the following steps:
Step 1: Multiply the whole number by the denominator.
Step 2: Add the result to the numerator.
Step 3: Keep the denominator the same.
Let's convert 1 ¾ back to an improper fraction:
- Multiply the whole number (1) by the denominator (4): 1 x 4 = 4
- Add the result (4) to the numerator (3): 4 + 3 = 7
- Keep the denominator the same (4)
Therefore, 1 ¾ = 7/4.
The Importance of Understanding Mixed Numbers
The ability to convert between improper fractions and mixed numbers is vital for various reasons:
- Simplified Calculations: Mixed numbers often make calculations simpler and more intuitive, especially when dealing with addition and subtraction of fractions. Imagine trying to add 11/8 + 5/8 directly versus adding 1 ¾ + 5/8. The latter is considerably easier.
- Real-World Applications: Many real-world situations require understanding mixed numbers. For instance, measuring ingredients in recipes (1 ½ cups of flour), calculating distances (2 ¾ miles), or working with dimensions in construction (3 ¼ inches).
- Foundation for Advanced Mathematics: A strong understanding of mixed numbers serves as a solid foundation for more advanced mathematical concepts, including algebra, geometry, and calculus.
Frequently Asked Questions (FAQ)
Q: Can all improper fractions be converted into mixed numbers?
A: Yes, all improper fractions can be converted into mixed numbers. This is because the numerator is always larger than the denominator, implying at least one whole unit is present.
Q: What if the remainder is zero after dividing the numerator by the denominator?
A: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 8/8 = 1. There's no fractional part.
Q: Why is it important to learn this?
A: Mastering the conversion between improper fractions and mixed numbers is essential for building a strong foundation in mathematics. It simplifies calculations, aids in understanding real-world measurements, and prepares you for more advanced mathematical concepts.
Q: Are there any shortcuts for converting improper fractions to mixed numbers?
A: While the step-by-step method is most reliable for understanding the concept, with practice, you can often perform the division and conversion mentally, especially for simpler fractions.
Conclusion
Converting 11/8 to a mixed number, resulting in 1 ¾, is more than just a simple mathematical operation. It’s a crucial stepping stone in understanding the relationship between fractions and whole numbers. This skill is not only essential for academic success but also for navigating everyday situations where fractions are commonly encountered. Through practice and a firm grasp of the underlying principles, you can confidently convert between improper fractions and mixed numbers, ensuring your success in mathematics and beyond. Remember to practice regularly; the more you practice, the more comfortable and proficient you'll become. The ability to visualize the conversion, as with the pizza example, is key to internalizing the concept. By understanding the "why" behind the process, you'll build a stronger and more enduring understanding of this fundamental mathematical skill.
Latest Posts
Latest Posts
-
Electric Field Of A Semicircle
Sep 17, 2025
-
Carbon Formula In Standard State
Sep 17, 2025
-
Atm To N Cm 2
Sep 17, 2025
-
Is South America Latin America
Sep 17, 2025
-
Convert 300 Kelvin Into Celsius
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 11/8 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.