0 X 2 6x 9
thesills
Sep 25, 2025 · 5 min read
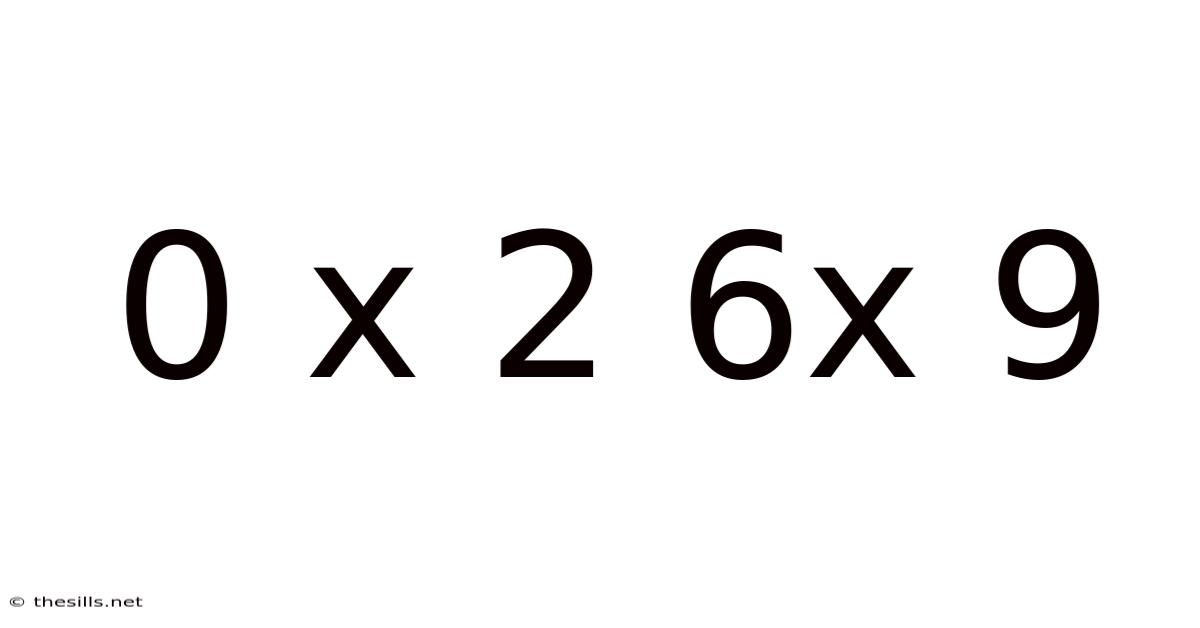
Table of Contents
Decoding 0 x 2 = 6 x 9: A Deep Dive into Mathematical Relationships and Problem-Solving
This article explores the seemingly paradoxical equation 0 x 2 = 6 x 9, examining its validity, the underlying mathematical principles, and its implications for problem-solving and critical thinking. We'll delve into the nuances of multiplication, zero's unique properties, and how apparent inconsistencies can lead to deeper mathematical understanding. While the equation itself, as presented, is incorrect, the exploration reveals valuable insights into the foundational concepts of mathematics. We will use this seemingly false equation as a springboard to uncover richer mathematical truths.
Understanding the Fundamentals: Multiplication and the Number Zero
Before dissecting the equation 0 x 2 = 6 x 9, let's refresh our understanding of basic arithmetic. Multiplication is essentially repeated addition. For instance, 3 x 4 means adding 3 four times (3 + 3 + 3 + 3 = 12). The numbers involved are called factors, and the result is the product.
Zero, a unique number in mathematics, plays a pivotal role. It's the additive identity; adding zero to any number doesn't change its value. However, its behavior in multiplication is equally important, but often misunderstood: any number multiplied by zero equals zero. This is a fundamental property of zero.
Why 0 x 2 ≠ 6 x 9: Addressing the Inaccuracy
The equation 0 x 2 = 6 x 9 is fundamentally incorrect. Let's break it down:
- 0 x 2 = 0: Applying the rule of multiplying by zero, the left side of the equation simplifies to zero.
- 6 x 9 = 54: The right side of the equation, calculated correctly, results in 54.
Therefore, the equation becomes 0 = 54, which is clearly false. The initial statement is incorrect because it violates the basic rules of arithmetic.
Exploring Potential Interpretations and Misconceptions
While the direct interpretation is false, we can explore potential misconceptions that might lead someone to believe such a statement. These misconceptions often stem from:
- Misunderstanding of Mathematical Symbols: A possible misunderstanding might involve the use of symbols. Incorrect interpretation of the "x" symbol for multiplication or a confusion of operational order might lead to erroneous calculations.
- Hidden Operations or Context: Perhaps the statement is part of a larger problem with additional hidden operations or contextual information that could change its validity. For example, it might be part of a word problem where some values are intentionally obscured or presented in a misleading way.
- Typographical Errors: It's possible that the presented equation contains a typographical error and the intended equation is something different, potentially leading to a correct solution.
Building a Bridge to Advanced Concepts: Exploring Related Mathematical Ideas
Though the given equation is incorrect, we can use this opportunity to explore related mathematical ideas that enhance our overall understanding:
- The Identity Property of Multiplication: The number 1 is the multiplicative identity; multiplying any number by 1 results in the same number. This is in contrast to zero's property.
- Distributive Property: This property states that a(b + c) = ab + ac. This property is crucial in algebraic manipulation and is often used in simplifying expressions.
- Order of Operations (PEMDAS/BODMAS): Understanding the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) is vital for solving complex mathematical expressions correctly. This order ensures consistent results regardless of who performs the calculation.
- Equation Solving: Incorrect equations, like the one presented, can be used as an excellent exercise in problem-solving. By analyzing why the equation is incorrect, we strengthen our abilities in identifying and correcting mathematical errors.
Developing Problem-Solving Skills: A Practical Approach
The erroneous equation 0 x 2 = 6 x 9 provides a valuable learning opportunity in developing critical thinking and problem-solving skills. The following steps highlight a practical approach:
- Identify the Problem: Clearly define the issue. The equation is presented as a statement of fact, but it is contradictory to fundamental mathematical principles.
- Analyze the Equation: Break down the equation step by step, evaluating each operation separately. Identify where the contradiction arises (0 ≠ 54).
- Investigate Potential Sources of Error: Consider potential misconceptions and alternative interpretations, like typographical errors or hidden context.
- Apply Mathematical Principles: Verify the equation using established mathematical principles such as the properties of zero, the order of operations, and the fundamental rules of arithmetic.
- Formulate a Conclusion: Clearly state the conclusion. The original equation is mathematically incorrect and violates fundamental arithmetic principles.
Frequently Asked Questions (FAQ)
- Q: Can zero ever equal another number? A: No, zero is a unique number and cannot equal any other number except itself.
- Q: Is there any mathematical context where 0 x 2 could be related to 6 x 9? A: No, in standard arithmetic, there is no valid context where these two expressions are equal. More complex mathematical structures might offer theoretical connections, but they would be far beyond the scope of this basic arithmetic context.
- Q: What is the importance of understanding the properties of zero? A: Understanding the unique properties of zero is crucial for mastering fundamental arithmetic and algebra. It avoids many common errors in calculations and problem-solving.
- Q: How can I improve my problem-solving skills in mathematics? A: Practice regularly, break down complex problems into smaller, manageable steps, and double-check your work. Understanding fundamental principles is vital, and reviewing common errors can significantly improve your accuracy.
Conclusion: Learning from Mistakes in Mathematics
While the equation 0 x 2 = 6 x 9 is demonstrably false, its analysis provides a valuable lesson. It highlights the importance of understanding fundamental mathematical principles, applying them correctly, and developing strong problem-solving skills. By identifying and correcting mathematical errors, we deepen our understanding of the subject and improve our ability to solve complex problems. Mistakes, in this context, are not failures, but opportunities for growth and learning. This exploration emphasizes the need for careful attention to detail and the importance of verifying results against established mathematical rules. Mathematics is a precise discipline, and a firm grasp of its foundations is crucial for success. Always question, always analyze, and always strive for accuracy.
Latest Posts
Related Post
Thank you for visiting our website which covers about 0 X 2 6x 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.