0.4 Percent As A Decimal
thesills
Sep 16, 2025 · 6 min read
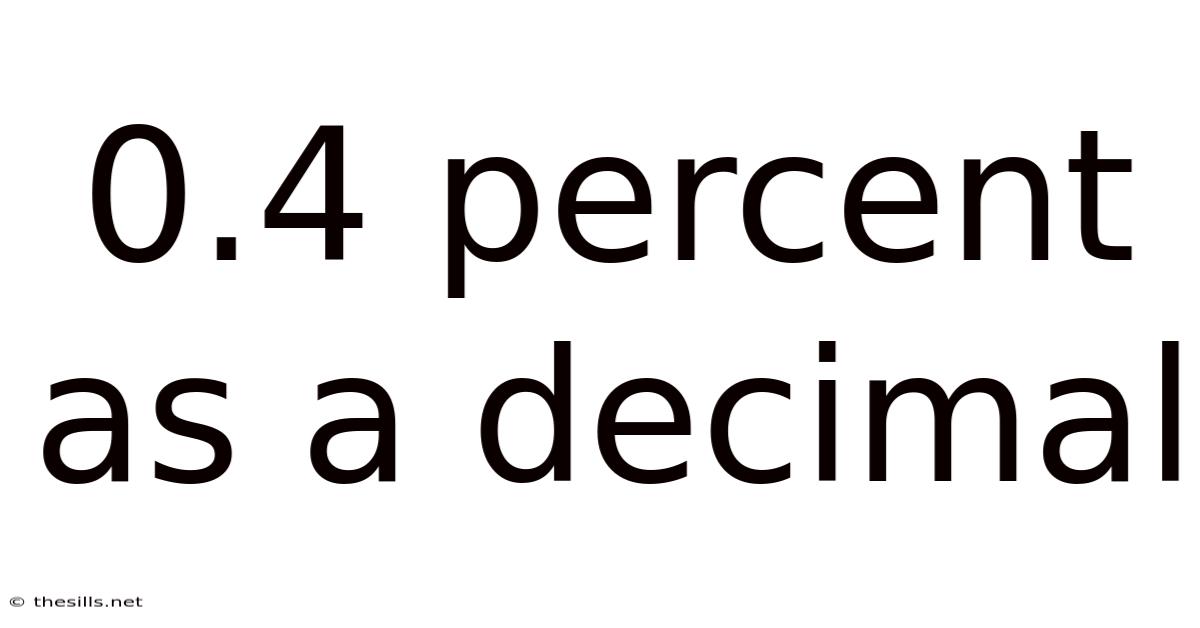
Table of Contents
Understanding 0.4 Percent as a Decimal: A Comprehensive Guide
Percentages are a common way to express fractions or proportions. Understanding how to convert percentages to decimals is a fundamental skill in mathematics, with applications spanning various fields like finance, statistics, and everyday calculations. This article will delve deep into understanding 0.4 percent as a decimal, exploring the underlying concepts, practical applications, and frequently asked questions. We will equip you with the knowledge and confidence to handle similar percentage-to-decimal conversions.
Understanding Percentages
Before we tackle 0.4 percent, let's review the core concept of percentages. A percentage is simply a fraction where the denominator is 100. For example, 50% means 50/100, which simplifies to 1/2 or 0.5. The percentage sign (%) is a shorthand way to represent this fraction.
The key to converting a percentage to a decimal lies in recognizing that the percentage sign essentially means "divided by 100." Therefore, to convert any percentage to its decimal equivalent, you simply divide the percentage value by 100.
Converting 0.4 Percent to a Decimal
Now, let's focus on converting 0.4% to a decimal. Following the rule mentioned above, we divide 0.4 by 100:
0.4 / 100 = 0.004
Therefore, 0.4 percent as a decimal is 0.004.
This simple calculation shows that 0.4% represents a very small fraction. It's important to understand the magnitude of this value in different contexts. For instance, in financial scenarios, 0.4% might represent a small interest rate or a minimal change in a stock price. In scientific contexts, it could represent a tiny measurement error or a subtle change in a chemical reaction.
Step-by-Step Guide to Converting Percentages to Decimals
To solidify your understanding, let's outline a step-by-step guide for converting any percentage to a decimal:
-
Identify the Percentage: Clearly identify the percentage you want to convert. In our case, it's 0.4%.
-
Remove the Percentage Sign: Remove the percentage sign (%). This leaves you with the numerical value, which is 0.4 in this example.
-
Divide by 100: Divide the numerical value obtained in step 2 by 100. This can be done easily by moving the decimal point two places to the left.
-
Write the Decimal Equivalent: The result of the division is the decimal equivalent of the original percentage. In our example, 0.4 divided by 100 equals 0.004.
Practical Applications of Percentage to Decimal Conversion
The ability to convert percentages to decimals is crucial in numerous real-world applications:
-
Finance: Calculating interest rates, compound interest, and understanding financial statements often require converting percentages to decimals. For example, calculating the interest earned on a savings account with a 0.4% annual interest rate requires converting 0.4% to its decimal equivalent (0.004).
-
Statistics: Many statistical calculations, such as calculating probabilities, standard deviations, and confidence intervals, involve working with percentages which are often expressed as decimals for calculations.
-
Science: In scientific research, experimental errors, measurement uncertainties, and changes in quantities are frequently expressed as percentages which then need to be converted to decimals for analysis and calculations.
-
Everyday Life: Understanding discounts, tax rates, and tips often involves working with percentages. Converting these percentages to decimals helps with quicker and more accurate calculations. For example, if a store offers a 0.4% discount, calculating the actual discount amount requires converting 0.4% to 0.004.
Understanding the Decimal System and Place Value
To fully grasp the concept of 0.004, let's briefly review the decimal system and place value. The decimal system is based on powers of 10. Each place value to the right of the decimal point represents a decreasing power of 10:
- Tenths (1/10): The first place after the decimal point represents tenths.
- Hundredths (1/100): The second place after the decimal point represents hundredths.
- Thousandths (1/1000): The third place after the decimal point represents thousandths.
In the decimal 0.004, the digit 4 is in the thousandths place. This means that 0.004 is equal to 4/1000, which simplifies to 1/250.
Advanced Concepts: Working with Larger and Smaller Percentages
While we've focused on 0.4%, the principles of percentage-to-decimal conversion remain the same for larger or smaller percentages.
For instance, converting 75% to a decimal involves dividing 75 by 100, which results in 0.75.
Conversely, converting a very small percentage like 0.02% involves dividing 0.02 by 100, resulting in 0.0002. The process remains consistent regardless of the size of the percentage.
Frequently Asked Questions (FAQ)
Q1: Can I convert a percentage to a decimal without dividing by 100?
A1: Yes, you can achieve the same result by simply moving the decimal point two places to the left. This is a shortcut that works because dividing by 100 is equivalent to moving the decimal point two places to the left.
Q2: What if the percentage is a whole number, like 25%?
A2: The process remains identical. You would divide 25 by 100, or move the decimal point two places to the left (assuming an implied decimal point after the 25), resulting in 0.25.
Q3: What if the percentage is greater than 100%?
A3: The process is the same. For instance, converting 150% to a decimal involves dividing 150 by 100, resulting in 1.5. Percentages greater than 100% represent values greater than 1.
Q4: How do I convert a decimal back to a percentage?
A4: To convert a decimal back to a percentage, simply multiply the decimal by 100 and add the percentage sign (%). For example, to convert 0.004 back to a percentage, you would multiply 0.004 by 100, resulting in 0.4%, illustrating the reversible nature of these conversions.
Q5: What are some real-world examples where this conversion is useful beyond finance and science?
A5: Many everyday situations involve percentage-to-decimal conversions. For example, calculating sales tax (e.g., a 6% sales tax becomes 0.06 for calculations), determining the discount on a sale item (e.g., a 20% discount becomes 0.20), or understanding the success rate of something (e.g., a 95% success rate becomes 0.95).
Conclusion
Converting 0.4 percent to its decimal equivalent, 0.004, is a straightforward process that relies on the fundamental understanding of percentages and the decimal system. Mastering this conversion is crucial for success in numerous fields, from finance and statistics to scientific research and everyday life. By understanding the underlying principles and practicing the steps, you'll be well-equipped to handle percentage-to-decimal conversions confidently and accurately. Remember, the key is to always divide the percentage value by 100, or equivalently, move the decimal point two places to the left. With practice, this will become second nature.
Latest Posts
Latest Posts
-
Which Of The Following Processes
Sep 16, 2025
-
Most Stable Conformation Of Butane
Sep 16, 2025
-
Is Subtraction Of Integers Commutative
Sep 16, 2025
-
Complete The Following Table Economics
Sep 16, 2025
-
1 X 1 Y 1
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 0.4 Percent As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.